Точка перетину медіан рівнобедреного трикутника віддалена від основи на 5 см а бісектриса кута при основі ділить висоту проведену до основи на відрізки у відношенні 5:4 обчислити периметр трикутника
Ответы
Ответ: Р = 90 см
Объяснение:
медианы точкой пересечения делятся в отношении 2:1, считая от вершины.
следовательно, медиана, проведенная к основанию (она же высота и биссектриса), = 15 см.
биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам; т.е.
b:(a/2) = 5:4 ---> b = 5a/8
или
b:(a/2) = 4:5 ---> b = 2a/5 -такого треугольника не существует; для любого треугольника должно выполняться неравенство треугольника: a<2b)
где a-основание равнобедренного треугольника; b-боковые стороны
по т.Пифагора
b^2 = (а/2)^2 + 15^2
(25/64)a^2 - (1/4)a^2 = 15^2
(9/64)a^2 = 15^2
a^2 = (15*8/3)^2
a = 40; b = 5*40/8 = 25
P = 2b+a = 50+40 = 90
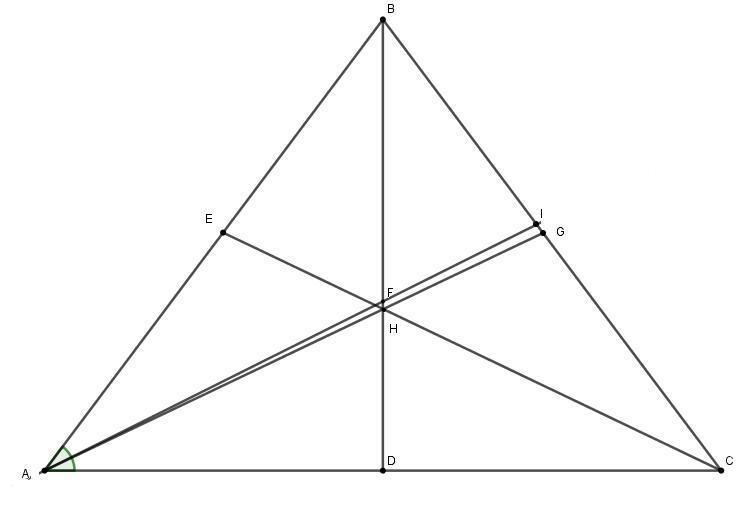
Точка F - точка пересечения биссектрисы угла при основании и высоты BD, H - точка пересечения медиан и делятся этой точкой на две части в отношении 2:1, считая от вершины.
HD = 5 см, следовательно BH = 2 * 5 = 10 см. Высота равнобедренного треугольника BD = 5 + 10 = 15 см.
Из условия BF/FD = 5/4 , пусть BF = 5x, тогда FD = 4x. Тогда по свойству биссектрисы для треугольника ABD
AB/AD = BF/FD = 5/4 ⇒ AB = 5y и AD = 4y
По теореме Пифагора из прямоугольного треугольника ABD
25y² = 16y² + 15²
9y² = 225
y = 5
Следовательно, AB = BC = 25 см и AC = 2*AD = 40 см.
Периметр ΔABC: P = AB + BC + AC = 25+25+40 = 90 см
Ответ: 90 см.