Предмет: Геометрия,
автор: dashamixdasha
гіпотенуза і один з катетів прямокутного трикутника дорівнюють 34 см і 30 см Знайти довжину перпендикуляра проведеного до гіпотенузи з її середини до перетину з більшим катетом
Ответы
Автор ответа:
1
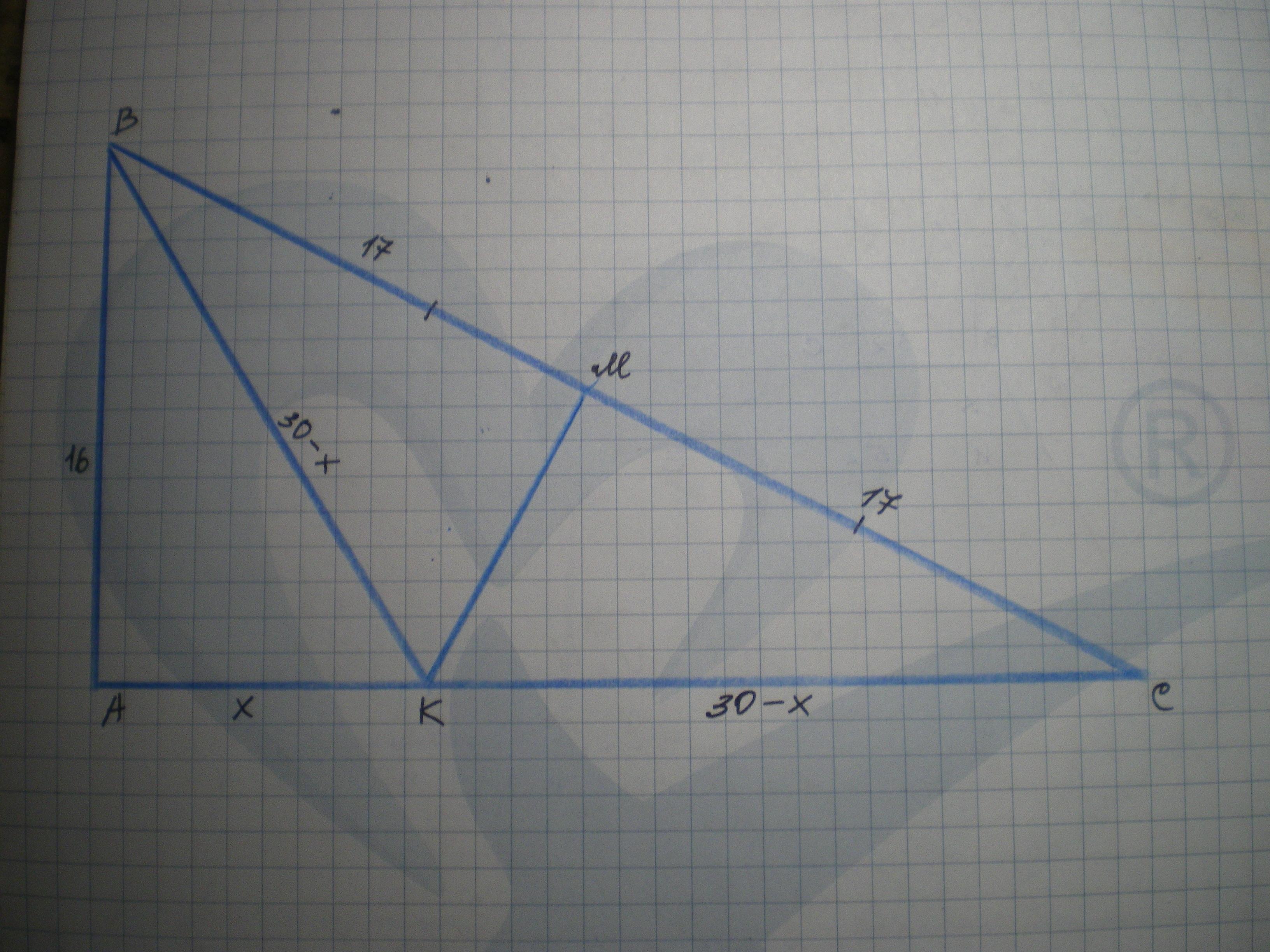
Дано: ΔАВС - прямокутний, ∠А=90°, АС=30 см, ВС=34 см; МК⊥ВС, ВМ=МС. Знайти МК.
Знайдемо АВ за теоремою Піфагора:
АВ=√(ВС²-АС²)=√(1156-900)=√256=16 см.
Проведемо ВК і розглянемо ΔВКС - рівнобедрений, тому що ВМ=СМ і МК⊥ВС, отже ВК=КС.
Нехай АК=х см, тоді КС=ВК=30-х см.
Знайдемо АК з ΔАВК - прямокутного:
АВ²=ВК²-АК²; 16² = (30-х)² - х²; 256=900-60х+х²-х²;
60х=900-256=644; х=10 11/15 см. АК=10 11/15 см, тоді
ВК = 30 - 10 11/15 = 19 4/15 = 289/15 см.
Знайдемо МК за теоремою Піфагора з ΔВМК, де ВМ=34:2=17 см.
МК²=ВК²-ВМ²=(289/15)² - 17² = (83521/225) - 289 = 18496/225.
МК=√(18496/225)=136/15=9 1\15 см.
Відповідь: 9 1/15 см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: adiyamukhambet
Предмет: Геометрия,
автор: troeshnik1234
Предмет: Литература,
автор: privet123321123
Предмет: Математика,
автор: evelinagafiatulina