Предмет: Алгебра,
автор: rockdog10293847
график функции 2x^2-(a+2)x+a пересекает ось Ox в точках x1 и x2, причем 1/x1 + 1/x2 = 3. Определите значение a и постройте график функции.
Ответы
Автор ответа:
20
Ответ:
Объяснение:
y = 2x^2 - (a+2)*x + a
У этой функции два корня, значит, D >=0
D = (a+2)^2 - 4*2*a = a^2 + 4a + 4 - 8a = a^2 - 4a + 4 = (a - 2)^2
x1 = (a+2 - (a-2))/4 = 4/4 = 1
x2 = (a+2 + (a-2))/4 = 2a/4 = a/2
У нас есть условие
1/x1 + 1/x2 = 3
1/1 + 2/a = 3
a = 1
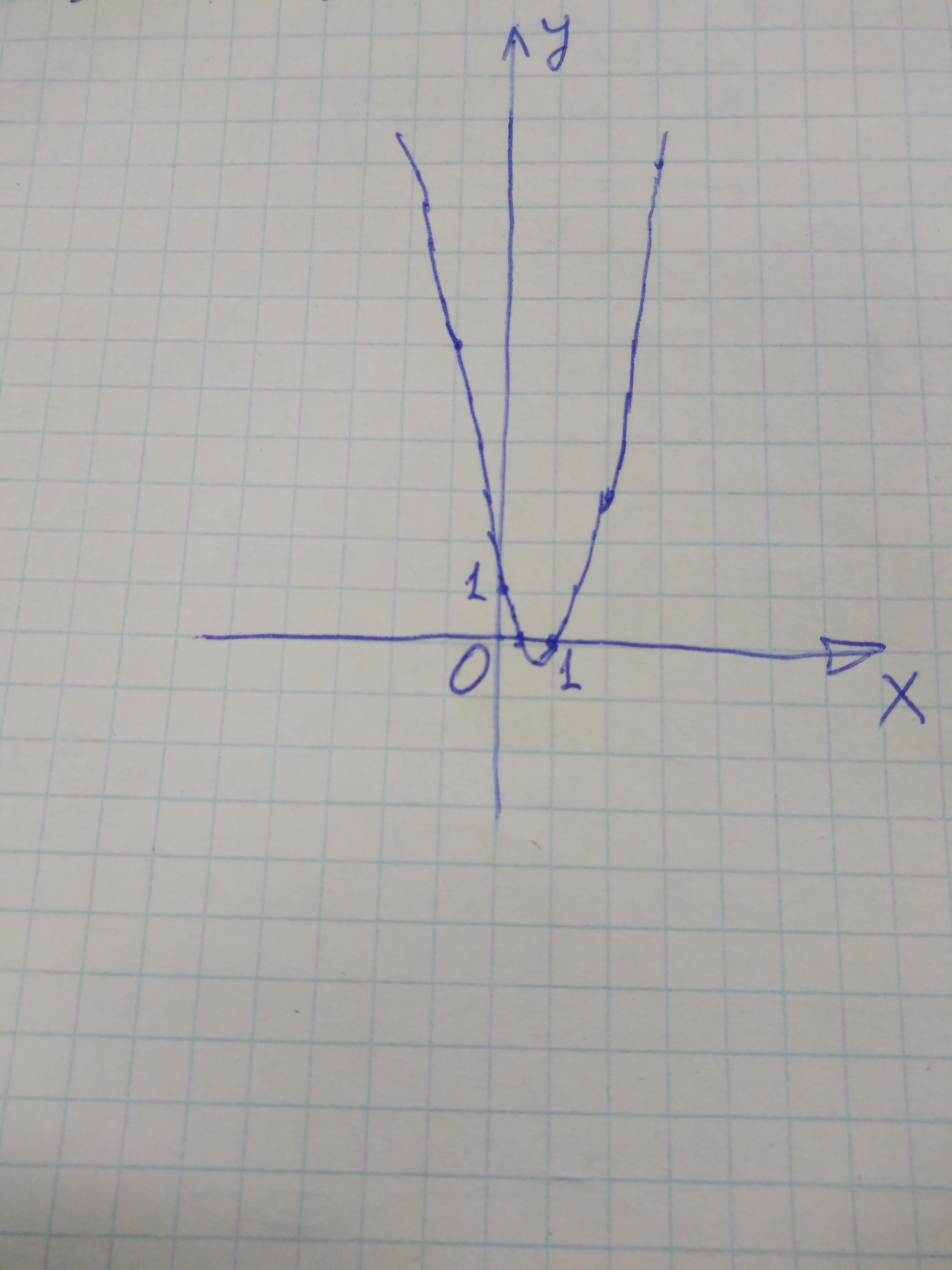
y = 2x^2 - 3x + 1
График на рисунке.
Приложения:
Аноним:
Проделана излишняя работа найдены корни, задача этого не требовала. Это не замечание к ответу, а записка на полях.
Я не понимаю, как найти а, не решая само уравнение.
(x1+x2)=3x1*x2 это из условия по т.Виета x1+x2=(a+2)/2 x1*x2=a/2 подставляя получим (a+2)/2=3a/2 откуда и найдем a.
Похожие вопросы
Предмет: Информатика,
автор: hasuliktar
Предмет: Алгебра,
автор: galuzovaksenya
Предмет: Химия,
автор: niktohaph
Предмет: Литература,
автор: Tanyaкрутышка