Question

помогите пожалуйста решить задание

Answer 1

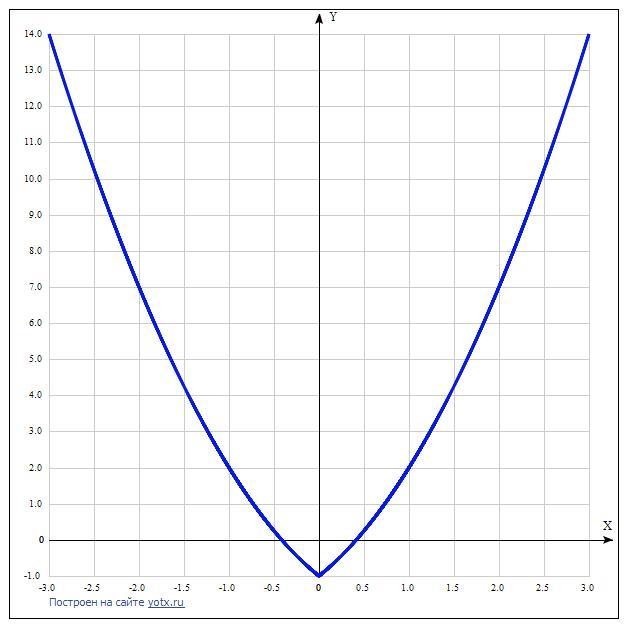
Дано уравнение х² + 2|x| - 1 = a.

Его можно считать аналогом обычного квадратного уравнения

у = ax² + bx + c. Графически - это парабола. Координате "у" соответствует параметр "а".

В этом уравнении второй член определяет сдвиг оси параболы вдоль координаты "х", а третий даёт точку пересечения графиком оси Оу.

В данной задаче второй член уравнения находится в модуле, то есть при разных знаках аргумента он не сдвигается, а, значит, остаётся на оси Оу.

Ветви параболы направлены вверх, значит, минимум находится на оси Оу, а это значение равно параметру "с". В нашей задаче - это значение -1 и оно одно.

Ответ: при а = -1 одно значение уравнения.