Предмет: Алгебра,
автор: jjsjs50
даю много баллов решите плиз.
Приложения:
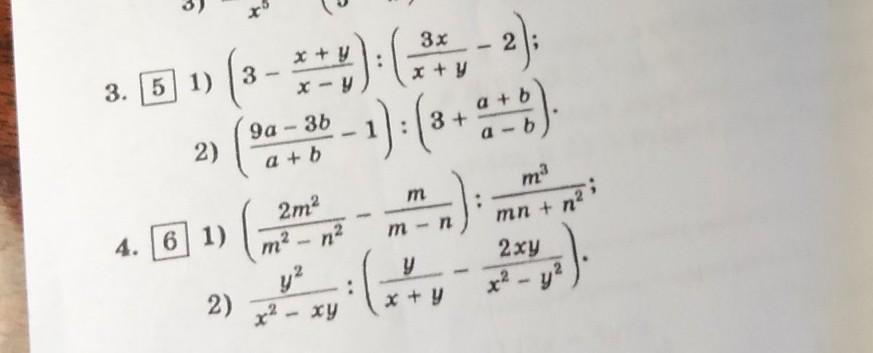
Ответы
Автор ответа:
1
3.
1)

2)

4.
1)

2)

1)
2)
4.
1)
2)
Похожие вопросы
Предмет: Қазақ тiлi,
автор: zbaessinova
Предмет: Литература,
автор: karina2009ufa
Предмет: Французский язык,
автор: Аноним
Предмет: Математика,
автор: vlad1042
Предмет: Математика,
автор: Аноним