Предмет: Алгебра,
автор: gghjjj88
решите плиз много баллов дам
Приложения:
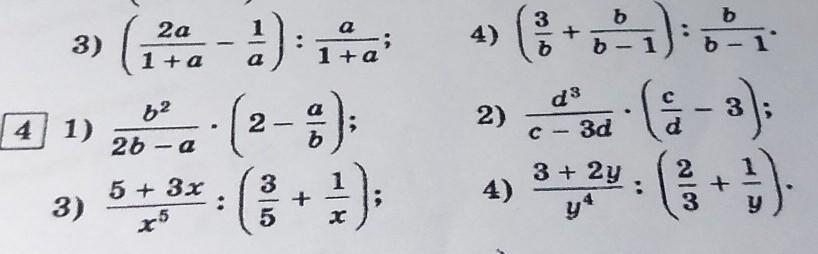
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Музыка,
автор: SaibotMK
Предмет: Алгебра,
автор: stashinantjnio
Предмет: Қазақ тiлi,
автор: pernebaevanargiza01
Предмет: Физика,
автор: вольт2201
Предмет: Алгебра,
автор: TKau