Предмет: Алгебра,
автор: Soltoevbek
Геометрическая прогрессия прошу помочь..Подробнее
Приложения:
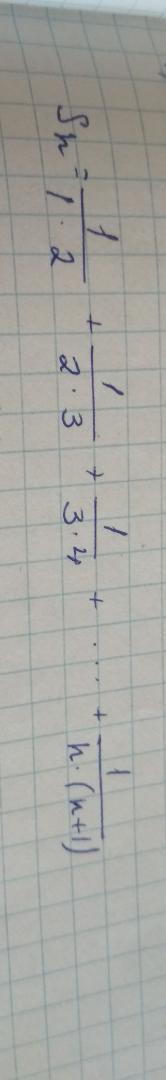
Аноним:
в числителе представьте как (n+1)-n
и разделите на две дроби
Ответы
Автор ответа:
1
Ответ:
Т.е. :
Автор ответа:
0
Ответ: 1 - 1/(n+1)
На мой взгляд, было бы правильно представить полученный результат в виде одной дроби.
Похожие вопросы
Предмет: Английский язык,
автор: murkaModnitca207
Предмет: Литература,
автор: vatryha7499
Предмет: Алгебра,
автор: lesch8926
Предмет: История,
автор: Sadagyk46
Предмет: Математика,
автор: ивангай94