Предмет: Геометрия,
автор: sbsivejwk
Условия, на фото помогите :(
Приложения:

Аноним:
задачка не сложная. Стоит теорию почитать и все)
Ответы
Автор ответа:
0
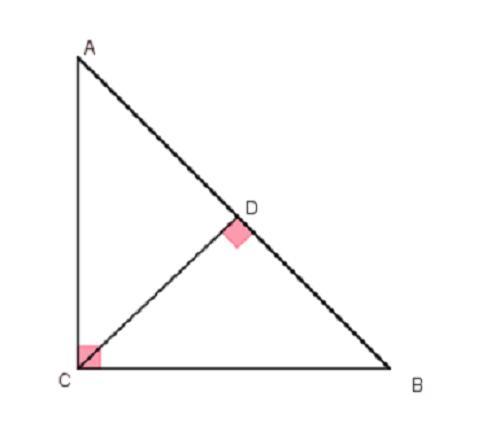
Треугольник АВС - прямоугольный (∠C = 90°), AC = 4 см, проекция катета ВС на гипотенузу равна 6 см. Найдите площадь треугольника ABC
Решение:
Пусть гипотенуза AB = x см, тогда AD = AB - BD = x - 6 см.
Катет есть среднее пропорциональное между проекцией катета и гипотенузой, то есть:
По теореме Виета
- не удовлетворяет условию;
см - длина гипотенузы AB
Тогда проекция катета АС на гипотенузу: AD = 2 см.
Высота, проведенная из прямого угла на гипотенузу, есть среднее пропорциональное между проекциями катетов.
см
Площадь треугольника ABC:
см²
Ответ: 8√3 см².
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Amilinamira
Предмет: Литература,
автор: mrkudasay
Предмет: Литература,
автор: juliyayuliyama
Предмет: Математика,
автор: Larmyna
Предмет: Химия,
автор: tuagunov