Question

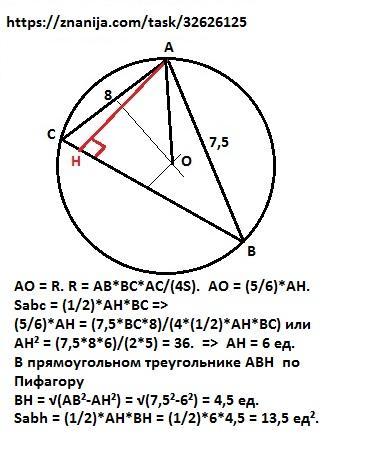
Около остроугольного треугольника АВС описана окружность с центром О. АН высота этого треугольника. АВ=7,5 ,АС=8, 5АН=6АО. Найдите площадь треугольника АВН.

Answer 1

Ответ:

Sabh = 13,5 ед².

Объяснение:

АО = R. R = AB*BC*AC/(4S).  AO = (5/6)*AH.  

Sabc = (1/2)*AH*BC =>

(5/6)*AH = (7,5*BC*8)/(4*(1/2)*AH*BC) или

АН² = (7,5*8*6)/(2*5) = 36.  =>  AH = 6 ед.

В прямоугольном треугольнике АВН  по Пифагору

ВН = √(АВ²-АН²) = √(7,5²-6²) = 4,5 ед.

Sabh = (1/2)*AH*BH = (1/2)*6*4,5 = 13,5 ед².

Answer 2

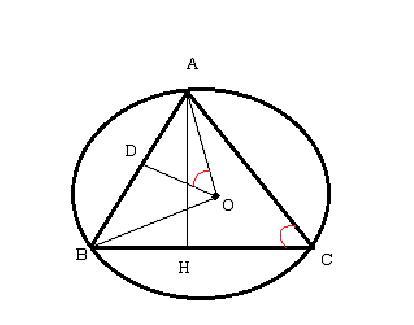
Проведем OD ⊥ AB, т.к. ΔAOB равнобедренный, то OD - биссектриса и медиана, следовательно, AD = DB = AB/2 = 15/4. ∠C - вписанный угол, опирающийся на дугу АВ, ∠АОВ - центральный и он в два раза больше вписанного угла BCA, т.е. ∠C = 0.5∠AOB, тогда ∠AOD = 0.5∠АОВ, следовательно, ∠AOD = ∠C ⇒ ΔAOD ~ ΔAHC (по двум углам). Из подобия треугольников следует, что $\sf \dfrac{AD}{AH}=\dfrac{AO}{AC}$

$\sf \dfrac{\dfrac{15}{4}}{\dfrac{6AO}{5}}=\dfrac{AO}{8}~~\Rightarrow~~~ AO^2=25~~~\Rightarrow~~~ AO=5;~~AH=\dfrac{6}{5}\cdot5=6$

По теореме Пифагора из прямоугольного треугольника ABH:

$\sf BH=\sqrt{AB^2-AH^2}=\sqrt{7.5^2-6^2}=\dfrac{9}{2}$

Площадь треугольника ABH:

$\sf S_{ABH}=\dfrac{1}{2}\cdot BH\cdot AH=\dfrac{1}{2}\cdot\dfrac{9}{2}\cdot6=\dfrac{27}{2}=13.5$ кв. ед.

Ответ: 13,5 кв.ед.