Предмет: Алгебра,
автор: kissfox27
Решите уравнение, пожалуйста!
Приложения:
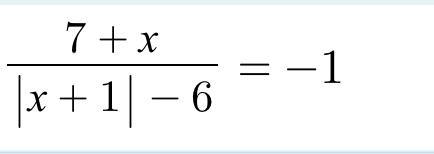
Ответы
Автор ответа:
1
- Найдём ОДЗ
- Первый случай
- Второй случай
Пересечём полученное множество с условием этого случая
- Объединим полученные решения
- Пересечём полученное множество решений с ОДЗ
Ответ.
Похожие вопросы
Предмет: Химия,
автор: gkler810
Предмет: Математика,
автор: asembaimakanova
Предмет: Геометрия,
автор: Anonim2667
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: sttelova12ulyana