Предмет: Математика,
автор: Evtushenkovadim2014
Решите СРОЧНО !!!!!!!! Производная функции
(Г)
Приложения:
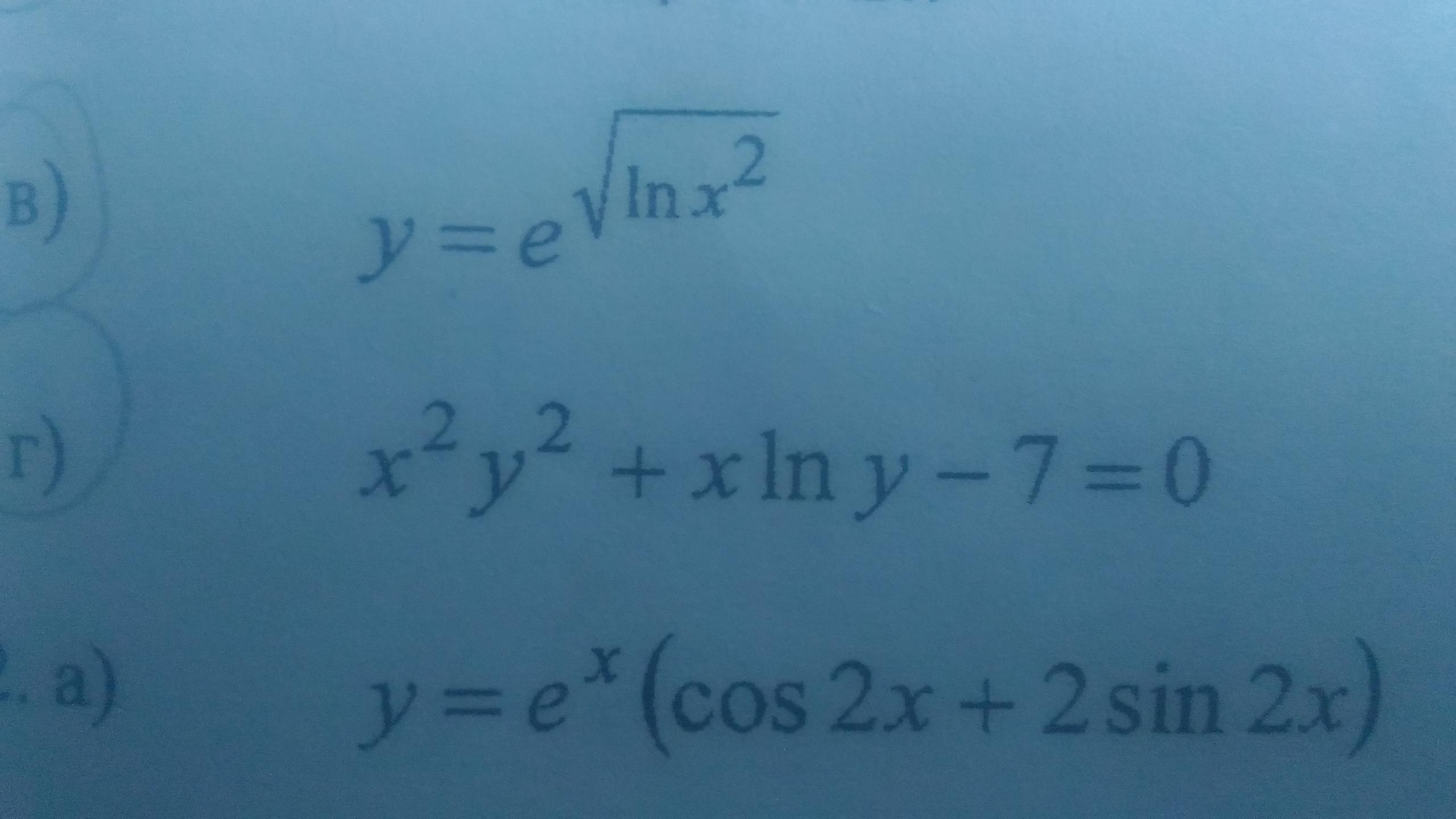
Evtushenkovadim2014:
а можно указать какие формулы использовались
Ответы
Автор ответа:
1
Г)
Ответ:
Приложения:
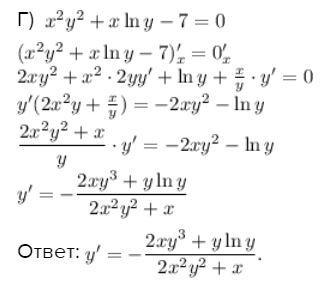
Укажите пожалуйста какие формулы использовались
Использовалось правило для неявной функции вида F(x; y)=0.
Чтобы найти производную неявной функции вида F(x;y)=0, необходимо продифференцировать обе части заданного уравнения, рассматривая функцию как функцию от х, а затем из полученного уравнения найти производную y'.
Уточнение: Чтобы найти производную неявной функции вида F(x;y)=0, необходимо продифференцировать обе части заданного уравнения, рассматривая функцию у как функцию от х, а затем из полученного уравнения найти производную y'. При решении производная функции у берется как производная сложной функции.
Похожие вопросы
Предмет: Математика,
автор: sofasemiceva3
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Математика,
автор: tokyarok
Предмет: Литература,
автор: элька106
Предмет: Математика,
автор: msgelya99