Предмет: Алгебра,
автор: elvirasalavatova
Помогите найти одз, пожалуйста.
Приложения:
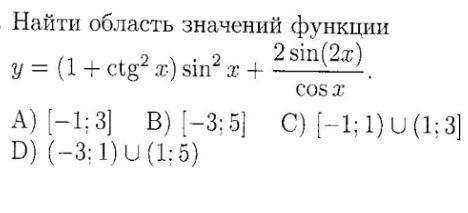
LFP:
найти ведь нужно не ОДЗ значения переменной (х)... а значения переменной (у)
Да,да, извините
Ответы
Автор ответа:
1
- Сначала найдем область определения функции
- Теперь равносильно (т.е. с учётом области определения) перейдем к новой функции
Поскольку изначально у нас есть ограничения на , а в полученной функции они отсутствуют, то, подставив запрещённые значения
в новую функцию, найдём выколотые точки
Т.к. мы прошли через всю единичную окружность, то значения функции начнут повторяться, следовательно, мы нашли все значения выражения
(Очевидно, что, выбрав отрицательное направление, мы обнаружим те же самые значения)
Значит, из множества значений новой функции нужно выколоть точки
- Найдем множество значений новой функции
- Выколем лишние точки
Ответ. D
Похожие вопросы
Предмет: Алгебра,
автор: LeshkaMazarov
Предмет: История,
автор: antymacc
Предмет: Математика,
автор: amaliya5064
Предмет: Литература,
автор: Lolkim
Предмет: Математика,
автор: zhostok1