Предмет: Математика,
автор: diana7618
Найти производную х’(f) параметрически заданной функции х=квадратный корень из 1-t в квадрате , у=t/квадратный корень из 1-t в квадрате
diana7618:
Ой производная y’(x)
Ответы
Автор ответа:
0
Ответ: t³ - t.
Приложения:
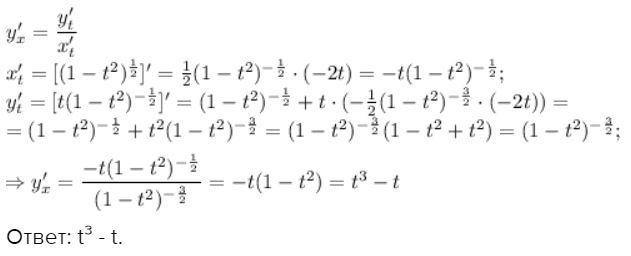
Похожие вопросы
Предмет: География,
автор: sergei27088
Предмет: Химия,
автор: morgenshternproPVP
Предмет: Русский язык,
автор: vladislavolekseenko8
Предмет: Физика,
автор: dzd16
Предмет: Физика,
автор: egorcnishov