Предмет: Математика,
автор: Корь
Решить тригонометрическое уравнение
Приложения:
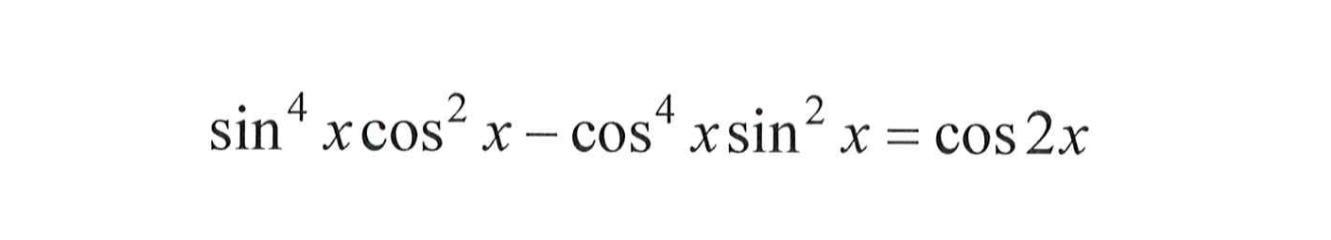
Ответы
Автор ответа:
0
Произведение двух множителей равно нулю ⇒
левая часть уравнения принимает только положительные значения., т.е. последнее уравнение решений не имеет.
Ответ:
Корь:
Откуда формула квадрата в последней строчке?
cos^2(x)sin^2(x) = (cos(x)*sin(x))^2 далее умножим и поделим на , т.е. (2*cos(x)*sin(x)/2)^2
Свойство степеней: a^n * b^n = (a*b)^n
Похожие вопросы
Предмет: Английский язык,
автор: kurganovvad
Предмет: Математика,
автор: 00varya00
Предмет: Литература,
автор: lololowka45
Предмет: Математика,
автор: icebaks
Предмет: Алгебра,
автор: poil3