Предмет: Алгебра,
автор: ALLAAA2
|ctg(2x-п/2)|=1/cos^2 2x -1
Help me please
Приложения:
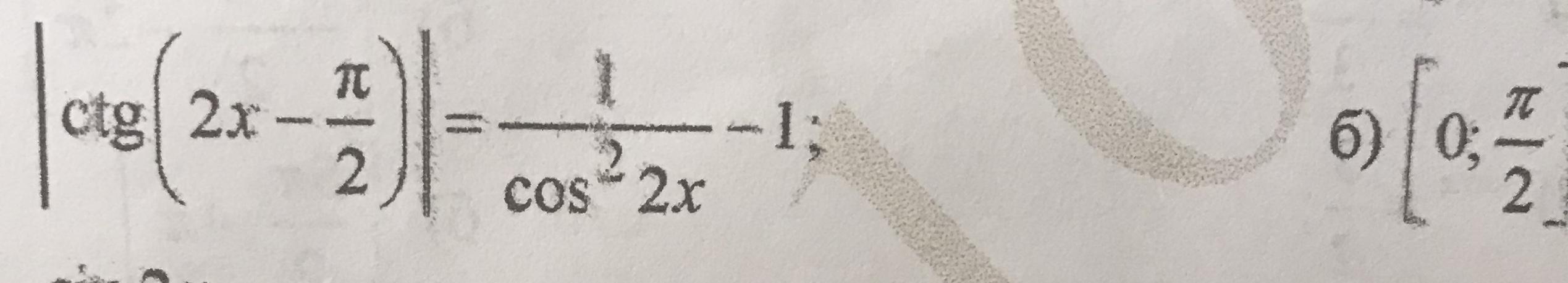
Ответы
Автор ответа:
6
Роман1233212002:
помогите пожалуйста с последним вопросом
Похожие вопросы
Предмет: Русский язык,
автор: CrazyVikiPiki
Предмет: Математика,
автор: kuzminakarina285gmai
Предмет: Математика,
автор: ksenanazarhyk
Предмет: История,
автор: УмняшкаMoget
Предмет: Информатика,
автор: OrAcUl