Предмет: Математика, автор: Vadim200129

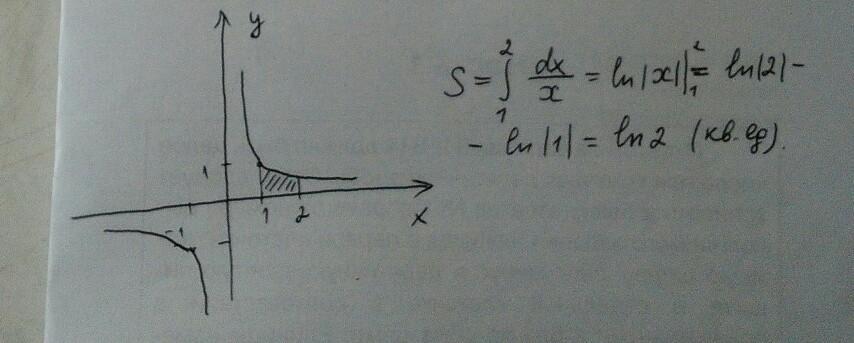
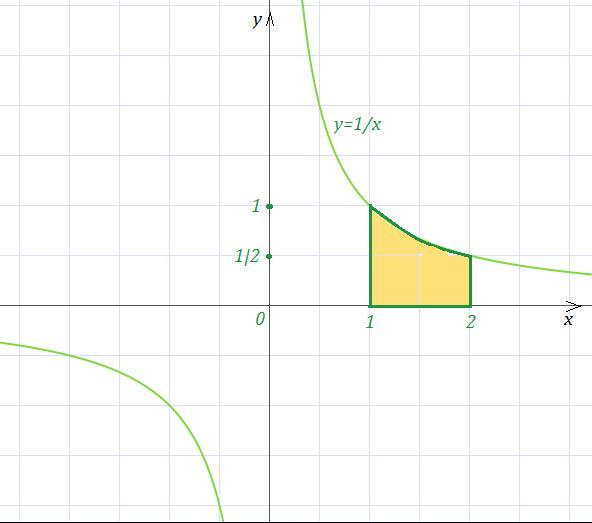
Вычислить площадь фигуры, ограниченной линиями y=1/x, x=1, x=2, y=0.

Ответы

Автор ответа: lilyatomach

1

Ответ:

решение представлено на фото

Приложения:

Автор ответа: NNNLLL54

0

$y=\frac{1}{x}\; \; ,\; \; x=1\; ,\; x=2\; \; ,\; \; y=0\\\\S=\int \limits _{a}^{b}\, f(x)\, dx=\int\limits^2_1\, \frac{1}{x}\, dx=ln|x|\, \Big |_1^2=ln2-\underbrace {ln1}_{0}=ln2$

Приложения:

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Математика, автор: tanyashulunova89

Найдите один неправильный ответ, а в случае его отсутствия

укажите: «Неправильного ответа нет».

А 1. Существенными признаками понятия «арифметическая задача» является наличие в тексте:

1) условия; 2) вопроса; 3) числовых данных;

4) реального сюжета; 5) взаимосвязи между условием и вопросом;

6) неправильного ответа нет.

А 2. В начальном обучении арифметические задачи выполняют следующие функции:

1) развитие разных видов мышления;

2) ознакомление с некоторыми математическими понятиями и закономерностями;

3) подготовка к жизни, в том числе к продолжению образования;

4) заучивание способов решения типовых задач;

5) воспитание некоторых качеств личности;

6) неправильного ответа нет.

А 3. На этапе ознакомления с арифметической задачей и ее структурой тексты задач полезно сравнивать с:

1) загадками;

2) короткими рассказами, где встречаются имена числительные или слово «сколько»;

3) математическими рассказами, где некоторая ситуация полностью описана на математическом языке;

4) задачами-шутками;

5) другими арифметическими задачами;

6) неправильного ответа нет.

А 4. Решить арифметическую задачу – это значит:

1) объяснить, какие действия и почему надо выполнить, чтобы найти требуемое в задаче;

2) вычислить;

3) сопоставить смысл полученного числа с требованием задачи;

4) проверить вычисления; 5) ответить на вопрос задачи;

6) неправильного ответа нет.

А 5. Решение любой арифметической задачи ведется по одному и тому же плану:

1) подготовительная работа;

2) восприятие и осмысление содержания задачи;

3) поиск и составление плана решения;

4) выполнение решения и ответ на вопрос задачи;

5) проверка;

6) работа над решенной задачей (творческая работа).

А 6. Обучение решению задач осуществляется поэтапно:

1) подготовительная работа;

2) работа по разъяснению текста задачи;

3) «открытие» арифметического способа решения задачи;

4) «взгляд назад» или рефлексия;

5) закрепление, т. е. формирование умения применять тот же способ в аналогичных задачах;

6) неправильного ответа нет.

А 7. В начальных классах арифметические задачи решаются следующими способами:

1) практическим; 2) арифметическим; 3) геометрическим;

4) алгебраическим; 5) подбора; 6) неправильного ответа нет.

А 8. Чтобы организовать на уроке решение задачи практическим способом, можно использовать:

1) полное иллюстрирование текста;

2) условно-предметное моделирование;

3) графическое моделирование;

4) краткую запись задачи;

5) неправильного ответа нет.

А 9. Чтобы «открыть» вместе с детьми арифметический способ решения задачи, можно:

1) полностью отказаться от наглядной интерпретации задачи;

2) проиллюстрировать только сюжет;

3) записать задачу кратко;

4) использовать предметное моделирование лишь части условия;

5) выполнить полное предметное моделирование текста задачи;

6) неправильного ответа нет.

А 10. В процессе обучения решению простых задач у учащихся формируются следующие общие умения:

1) выразительно читать; 2) выделять условие и вопрос;

3) обоснованно выбирать арифметическое действие, соответствующее описанной в тексте взаимосвязи между данными и искомым;

4) использовать для выбора арифметического действия и обоснования его правильности различные виды моделей;

5) оформлять запись решения; 6) применять способы проверки.

5 лет назад

Предмет: Английский язык, автор: faizulinmarat403

Помогите пожалуйста пж

5 лет назад

Предмет: Другие предметы, автор: vladosik144

Які вади є найпоиренішими на нашій планеті?

5 лет назад

Предмет: Литература, автор: superdudkaira

Написать названия сказок, о героях которых можно сказать:" друг- дороже денег", "доброе братство лучше богатства."

8 лет назад

Предмет: Алгебра, автор: qwertyuiop2110

x^2+y^2=10
x+y=-4
решите систему уравнений

8 лет назад