Предмет: Математика,
автор: Dusfix
Супер срочно отдам все что есть
17 баллов
Приложения:
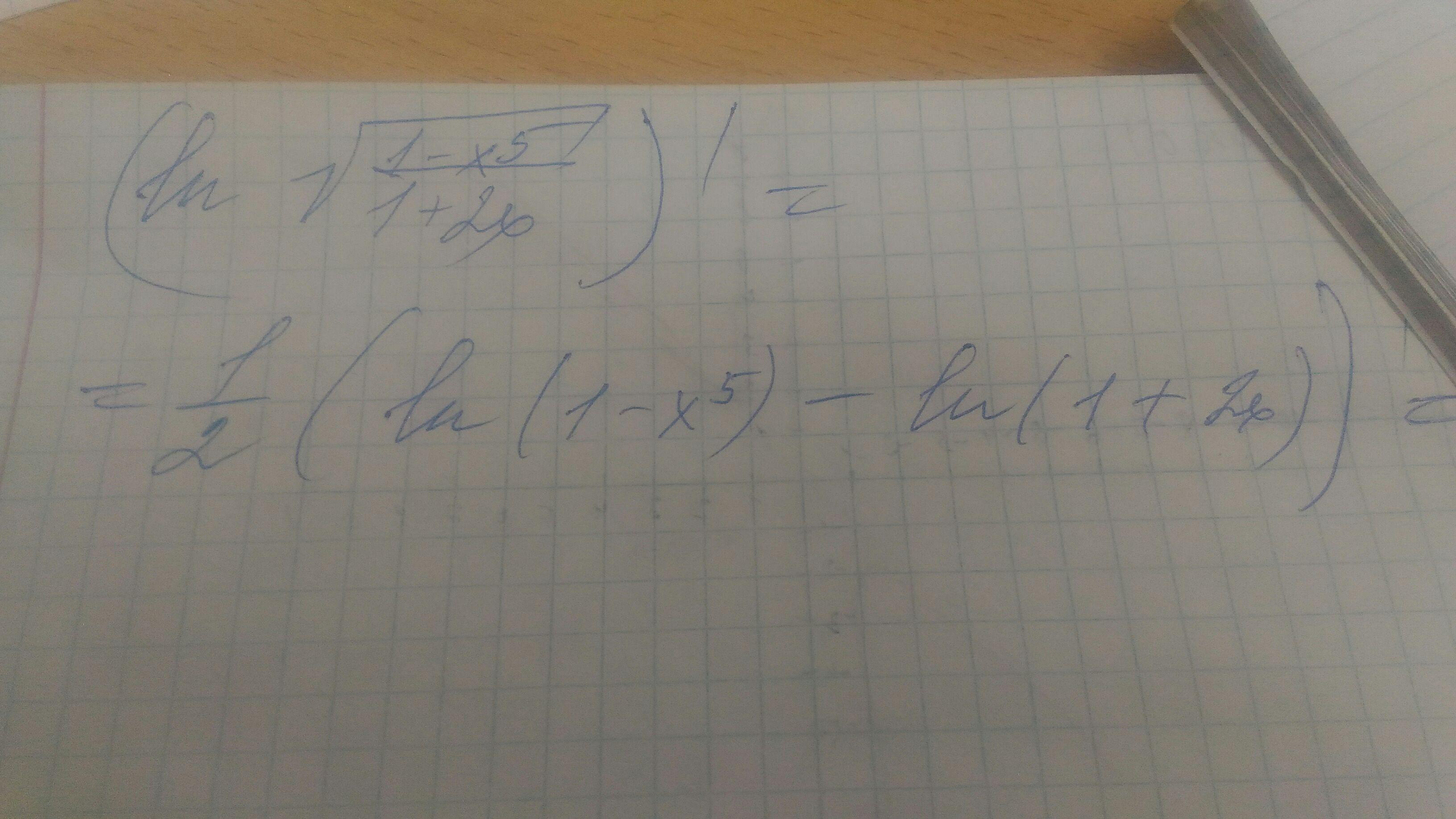
Ответы
Автор ответа:
0
Ответ: р
решение представлено на фото
Приложения:
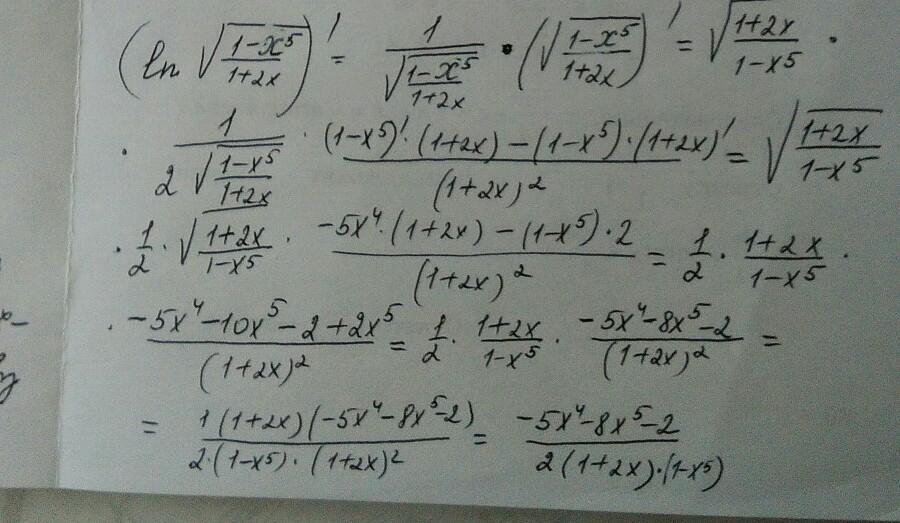
NNNLLL54:
В конце в знаменателе забыли дописать множитель
спасибо
Автор ответа:
1
Похожие вопросы
Предмет: Окружающий мир,
автор: ilonashaff
Предмет: Українська мова,
автор: vikaodizna
Предмет: Алгебра,
автор: Ulianakorneeva4838
Предмет: Математика,
автор: mashenkailkiv1
Предмет: Математика,
автор: лолита58