Предмет: Алгебра,
автор: lanabanana934
Как сделали переход от тангенса к синусу? Через какую формулу? Если кому-то нужно полное решение, то на 2 фотографии(хотя это понадобится)
Приложения:
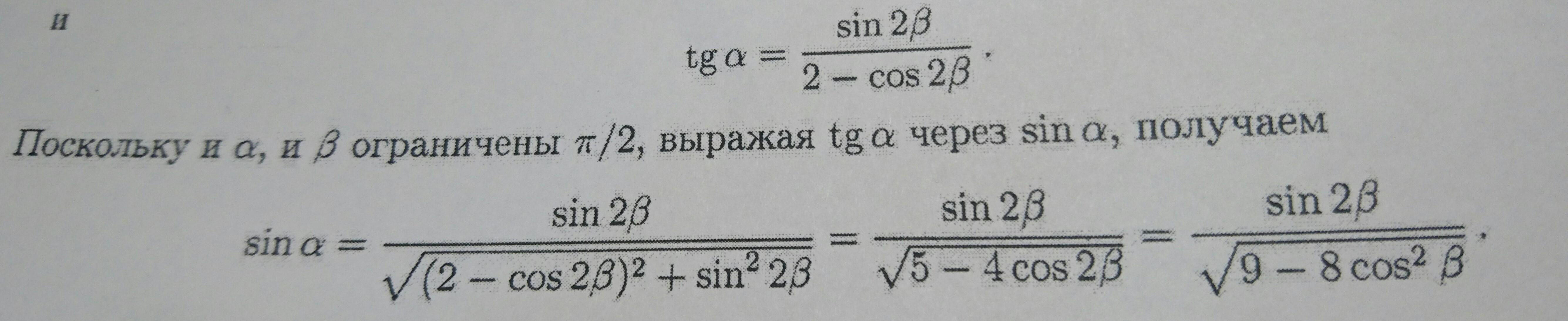

LFP:
записали определение: tgx=sinx/cosx; заменили косинус на +V(1-sin^2x); возвели обе части равенства в квадрат: tg^2x=sin^2x/(1-sin^2x) и выразили отсюда синус в квадрате через тангенс в квадрате... tg^2x-tg^2x*sin^2x=sin^2x... tg^2x=sin^2x*(1+tg^2x) ---> sinx=tgx/V(1+tg^2x)
Ответы
Автор ответа:
0
На втором фото есть выражение, сразу наж формулой для тангенса. Синус переносим в правую часть, потом на синус альфа делим, и слева получаем тангенс.
Справа получаем sin(2b) и знаменатель.
Искомая формула получается, потому что
а эта формула справедлива, как легко видеть, если расписать квадрат синуса. Проделайте это самостоятельно!
Похожие вопросы
Предмет: Английский язык,
автор: pupiiiq
Предмет: Математика,
автор: simonyananna74
Предмет: Литература,
автор: mrshtripx
Предмет: География,
автор: len4ik9
Предмет: Математика,
автор: оли9