Предмет: Алгебра,
автор: inkamove
Доведіть, що  + 5
+ 5 + 4ху – 4у + 4
+ 4ху – 4у + 4  0 при усіх дійсних значеннях х і у.
0 при усіх дійсних значеннях х і у.
Ответы
Автор ответа:
3
Доказательство:
х^2 + 5у^2 + 4ху - 4у + 4 ≥ 0
(х^2 + 4у^2 + 4ху) + (у^2 - 4у + 4) ≥ 0
(х^2 + (2у)^2 + 2•х•2у) + (у^2 - 2•2•у + 2^2) ≥ 0
(х + 2у)^2 + (у - 2)^2 ≥ 0
Так как (х + 2у)^2 ≥ 0 и (у - 2)^2 ≥ 0 при всех
ДЕЙСТВИТЕЛЬНЫХ значениях х и у, то и их сумма (х + 2у)^2 + (у - 2)^2 ≥ 0 при всех
ДЕЙСТВИТЕЛЬНЫХ значениях х и у, что и требовалось доказать.
Автор ответа:
1
Ответ:
решение представлено на фото
Объяснение:
Приложения:
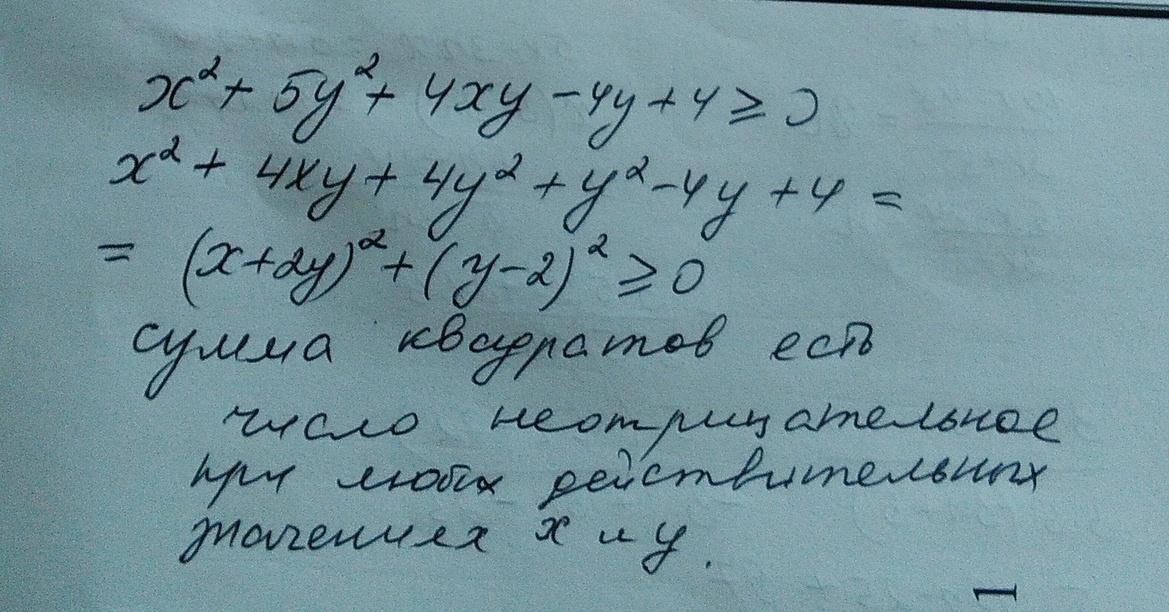
Похожие вопросы
Предмет: Математика,
автор: rodomansasa341
Предмет: Математика,
автор: omaznxp
Предмет: Українська мова,
автор: dimamoroz2509
Предмет: Геометрия,
автор: yablokoboss