Предмет: Алгебра,
автор: dakrinas
При каких значениях параметра а система уравнений не имеет решений?
Приложения:

новичок0:
Решаешь вступительные в МЭИ? ахаха
Ответы
Автор ответа:
1
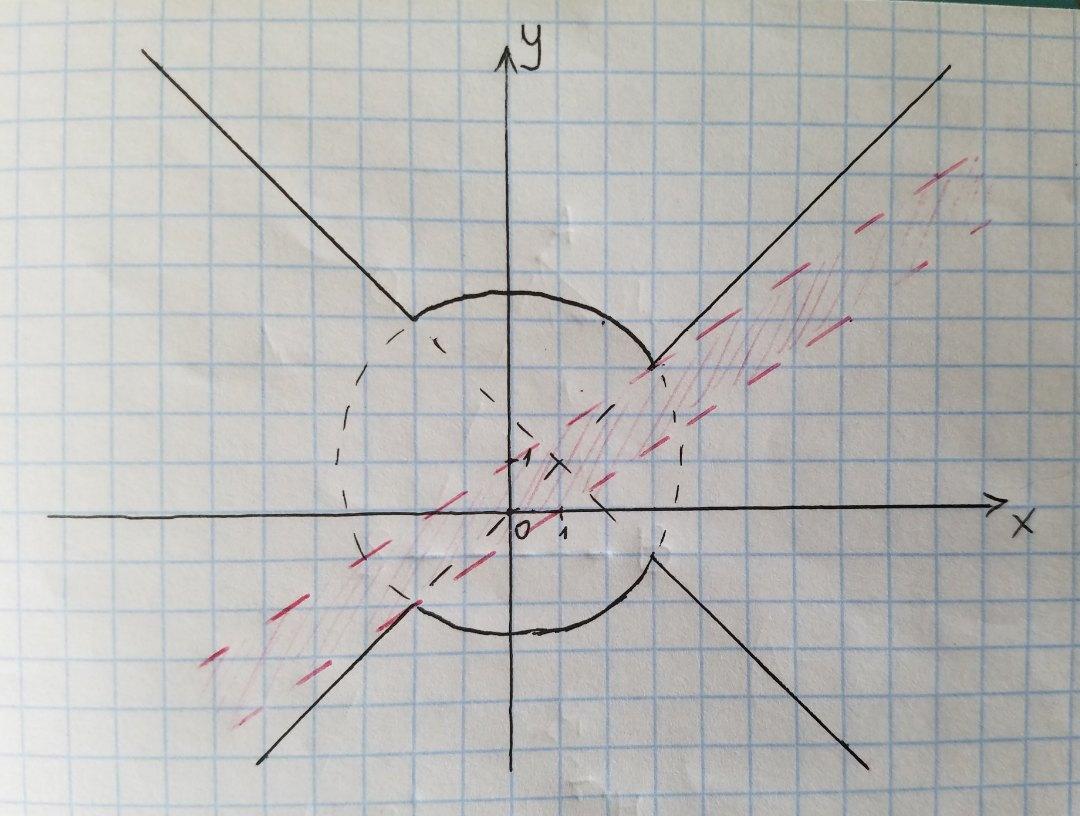
Начертим график первого уравнения:
При :
При :
Это уравнение окружности с центром в точке (0; 1) и радиусом √13.
Второе уравнение — прямая с коэффициентом . Он меньше 1, поэтому при некоторых значениях параметра прямая как бы пролетает сквозь дыру в первом графике, то есть система не имеет решений.
Система "начинает" иметь решения, когда прямая проходит через точки (3; 3) и выше или (-2; -2) и ниже. Нам нужно, чтобы прямая находилась между этими точками. Найдём граничные значения a:
Ответ:
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: tooptoopk
Предмет: Английский язык,
автор: serklkasperskij
Предмет: Геометрия,
автор: Аноним
Предмет: Математика,
автор: kotouha