Решить пару тригонометрических уравнений
По-подробнее, если можно, спасибо ;-)
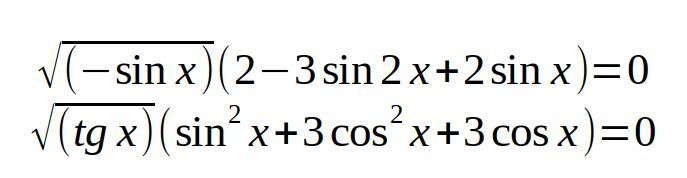
Ответы
Ответ:
Пошаговое объяснение:
1) Произведение равно нулю, когда один из множителей равен нулю, а другой существует. На основании этого составим систему:
√(-sin(x)) = 0 или -sin(x) > 0 и 2 - 3sin(2x) + 2sin(x) = 0
Решим последнее уравнение:
2 - 3sin(2x) + 2sin(x) = 0
3sin(2x) - 2sin(x) - 2 = 0
6sin(x)cos(x) - 2sin(x) - 2 = 0 | :2
3sin(x)cos(x) - sin(x) - 1 = 0
3sin(x)cos(x) = 1 + sin(x)
(3sin(x)cos(x))² = (1 + sin(x))²
9sin²(x)(1-sin²(x)) = 1 + sin²(x) + 2sin(x)
9sin²(x) - 9sin^4(x) = 1 + sin²(x) + 2sin(x)
9sin^4(x) - 8sin²(x) + 2sin(x) +1 = 0
Обозначим sin(x) = t, тогда уравнение примет вид:
9t^4 - 8t² + 2t + 1 = 0
Заметим, что t = -1 - решение. Тогда, выполнив деление, разобьем на множители:
(t + 1)(9t³ - 9t² + t + 1) = 0
Произведение равно нулю, когда один из множителей равен нулю. Рассмотрим кубическое уравнение:
9t³ - 9t² + t + 1 = 0 | * 3
27t³ - 3 * 9t² + 3t + 3 = 0
(3t)³ - 3 * (3t)² + 3t + 3 = 0
Пусть 3t = m, тогда:
m³ - 3m² + m + 3 = 0
Выделим полный куб:
m³ - 3m² + 3m - 1 - 2m + 4 = 0
(m - 1)³ - 2m + 4 = 0
Пусть m - 1 = y, тогда m = y + 1:
y³ - 2(y + 1) + 4 = 0
y³ - 2y + 2 = 0
p = -2; q = 2
Согласно формуле Кардано:
Q = (q/2)² + (p/3)³ = 1 - 8/27 = 19/27.
√Q = √57/9
y = ∛(-q/2 + √Q) + ∛(-q/2 - √Q) = ∛( -1 + √57/9) - ∛(1 + √57/9)
m = y + 1 = ∛( -1 + √57/9) - ∛(1 + √57/9) + 1
t = m/3 = 1/3 * (∛( -1 + √57/9) - ∛(1 + √57/9) + 1) = sin(x)
Очевидно, данное число больше нуля, а поэтому, оно нас не устраивает по ОДЗ (sin(x) ≤ 0)
Значит, корень единственнен - t = -1.
Выполним обратную замену: t = sin(x)
sin(x) = -1
x = -π/2 + 2πn
Так же решим первое уравнение системы:
√(-sin(x)) = 0
sin(x) = 0
x = πk.
Ответ: x = -π/2 + 2πn; x = πk.
-----------------------
2) √tg(x) ( sin²(x) + 3cos²(x) + 3cos(x)) = 0
Произведение равно нулю в том случае, когда один из множителей равен нулю, а остальные существуют:
либо tg(x) = 0, либо sin²(x) + 3cos²(x) + 3cos(x) = 0 и tg(x) > 0
Решим второе уравнение:
sin²(x) + 3cos²(x) + 3cos(x) = 0
sin²(x) + cos²(x) + 2cos²(x) + 3cos(x) = 0
1 + 2cos²(x) + 3cos(x) = 0
D = 9 - 8 = 1
cos(x) = (-3 ± 1)/4 = -1 или -0.5
cos(x) = -1 ⇒ x = π + 2πn
cos(x) = -0.5 ⇒ x = ±(2/3π) + 2πk
Из ОДЗ следует, что tg(x) ≥ 0, а значит, углы принадлежат I и III четвертям.
Значит, нам подходят: x = π + 2πn, а так же -2/3π + 2πk.
Теперь решим уравнение:
tg(x) = 0.
x = π/4 + πm.
Ответ: x = π + 2πn, x = -2/3π + 2πk. x = π/4 + πm.