Предмет: Алгебра,
автор: Gwen10
Решите неравенство с модулями
Приложения:
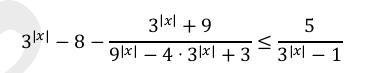
Ответы
Автор ответа:
1
Ответ:
решение представлено на фото
,
Приложения:

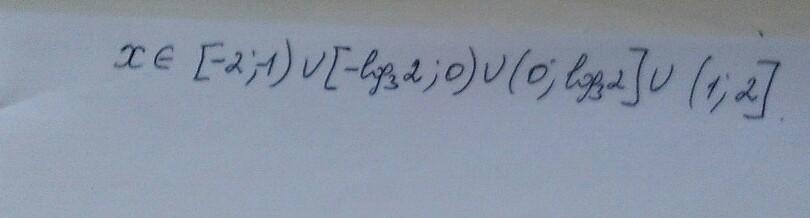
Автор ответа:
1
Пусть , тогда
Ответ:
Похожие вопросы
Предмет: Математика,
автор: daradikun9
Предмет: Математика,
автор: danatzusupov021
Предмет: Геометрия,
автор: rita8181818199101
Предмет: Математика,
автор: Эдик10лет