Найди площадь равнобедренного треугольника, основание которого равно 8, а боковая сторона 5.
1) 40
2) 18
3) 12
4) 24
Сделайте пожалуйста с чертежом, спасибо)
Ответы
Если ∆ ABC- равнобедр., а 1-я боковая сторона АB=6 , то и другая боковая сторона BC=6.Проведем из вершины B биссектрису BH к основанию AC, а в равнобедренном ∆ биссектриса является и медианой и высотой. Образовались два прямоугольных ∆ :
∆ ABH
∆ BHC c катетами 4 AH и BC, т.к BH- это медиана и медиана делит сторону пополам. По теореме Пифагора :
ВН² + 4² = 5²
ВН² = 25 - 16
ВН² = 9
ВН = 3.
S ∆-a = 1/2 × 3 × 8 = 12.
Ответ : S = 3) 12 см².
_________________________________
Удачи✨)))))
Ответ:
3) 12
Объяснение:
Дано:
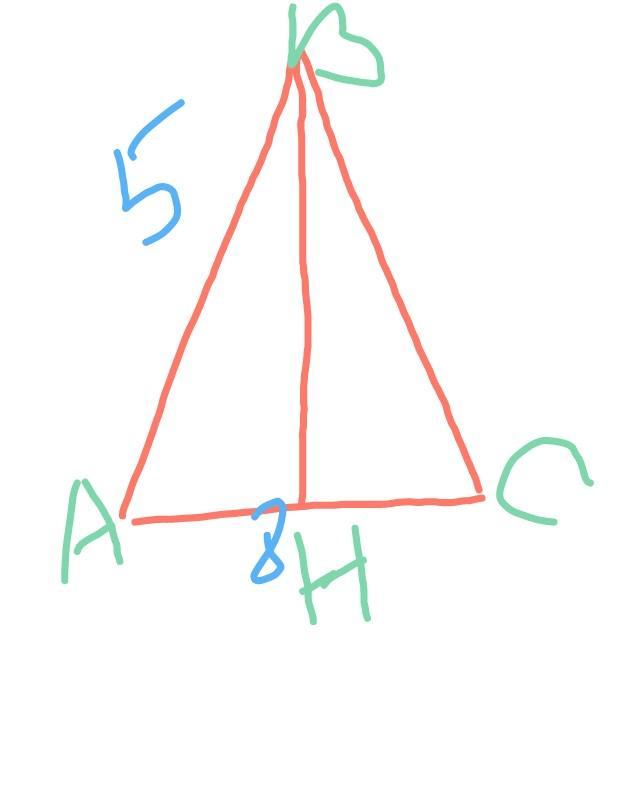
ABC — равнобедренный треугольник;
АВ = 5, АС = 8
S∆ABC — ?
Решение:
Так как , ∆АВС — равнобедренный, боковые стороны равны = 5 ;
Опустим из вершины В на основание АС высоту BH.
Так как высота равнобедренного треугольника делит его основание пополам, то длина половины основания будет равна:
АН = АС / 2 = 8 / 2 = 4
Высота с половиной основания и стороной равнобедренного ∆ образует прямоугольный треугольник АВН.
По теореме Пифагора выразим длину второго катета, он и будет высотой ∆ АВН:
ВН = √ ( 5² - 4² ) = √ ( 25 - 16 ) = √9
ВН = 3;
Для нахождения площади прямоугольного треугольника используем формулу : S = ½ * BH * AC
S = ½ * 3 * 8 = 12
~•~•~•ZLOY_TIGROVSKIY~•~•~•
по теореме Пифагора V( 5^2-4^2)=V9=3
высота 3 см
S=(3*8)\2=12