Question

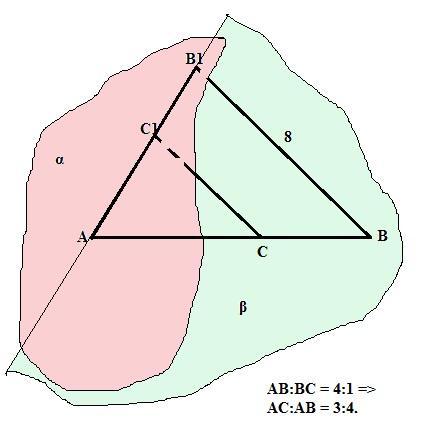
через конец А отрезка AB проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые, которые пересекают плоскость соответственно в точках B1 и C1. Найти длину отрезка СС1, если AB: BC=4:1, ВВ1=8 см.​

Answer 1

Ответ:

СС1 = 6 см.

Объяснение:

Через конец А отрезка AB проведена плоскость α.

Через две параллельные прямые можно провести плоскость, и при том только одну. Пусть это плоскость β. Прямая АВ, естественно, лежит в этой плоскости.  => Плоскость α пересекается плоскостью β по прямой АВ1 и треугольники АС1С и АВ1В, лежащие в плоскости β, подобны (так как ВВ1 параллельна СС1) с коэффициентом подобия k = AC/AB = 3/4 (так как АВ=4х, а ВС =х -дано, то АС=3х).

Из подобия имеем: СС1 = BB1*k = 8*3/4 = 6 см.