Question

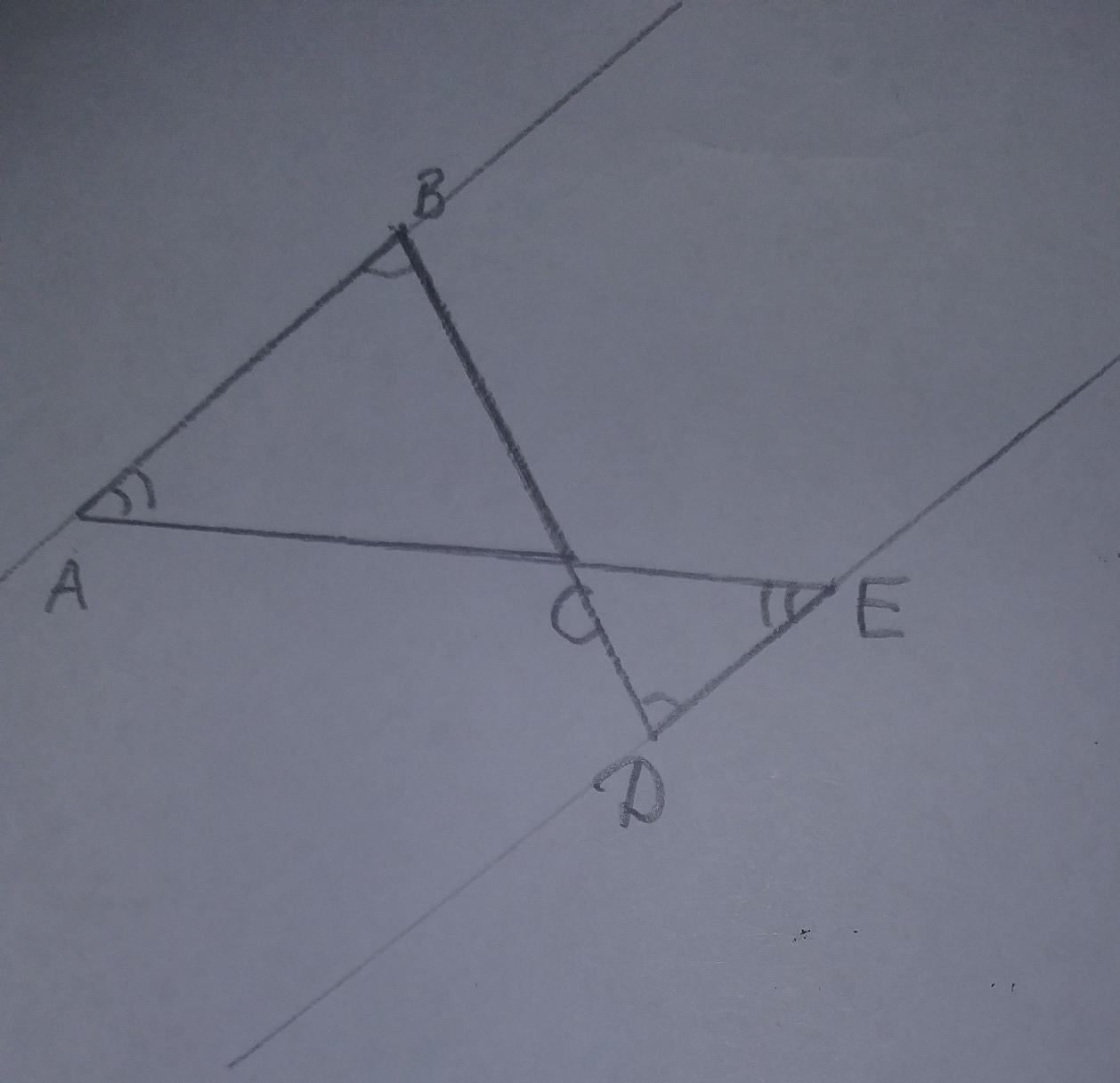
в треугольнике ABC AC = 16 и ВС = 12. На продолжениях
сторон AC и BC за точку С отмечены точки E и D соответственно так, что прямые DE и AB параллельны. Найдите СЕ,
если CD = 6.​

Answer 1

Ответ:

Объяснение:

Если АВ II DE, тогда:

1) угол ВАС = углу DEC(тк. накрест лежащие углы)

2) угол АВС = углу EDC(аналогично)

Теперь рассмотрим треугольники АВС и EDC:

треугольник АВС~ЕDC по двум равным углам.

Значит:

$\frac{ab}{ed} = \frac{bc}{dc} = \frac{ac}{ec}$

Нам нужно только второе и третье из равенства:

$\frac{bc}{dc} = \frac{ac}{ec} \\ \frac{12}{6} = \frac{16}{ec} \\ ec = 8$

Answer 2

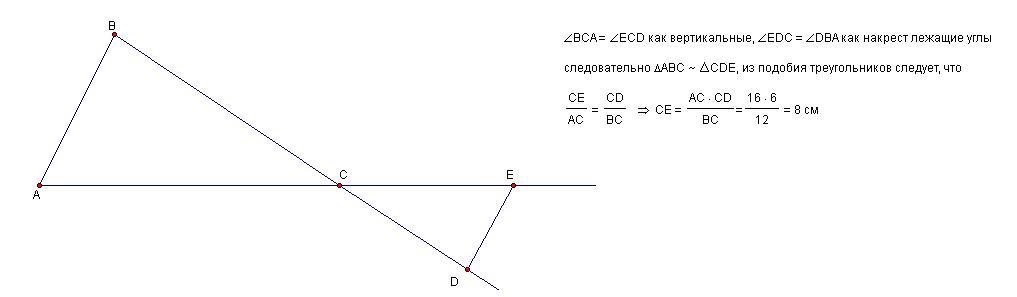
Ответ: 8.

Объяснение: