Предмет: Алгебра,
автор: viktoriaserebrian
решите пожалуйста эти задачи
Приложения:


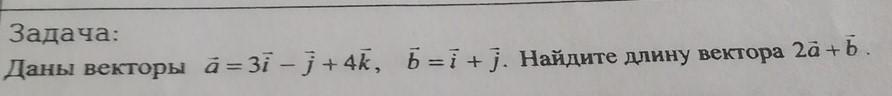
Ответы
Автор ответа:
2
Ответ:
Объяснение:
1 задача. Предел
2 задача. Область определения.
{ |x|/2 - 4 ∈ [-1; 1]
{ arccos (|x|/2 - 4) ≠ 0
Решаем
{ |x|/2 ∈ [3; 5]
{ |x|/2 - 4 ≠ 1
Получаем
{ |x| ∈ [6; 10]
{ |x|/2 ≠ 5
10 не входит из-за второго уравнения.
|x| ∈ [6; 10)
x ∈ (-10; -6] U [6; 10)
3 задача. Векторы.
a = {3i - j + 4k}; b = i + j. Найти 2a + b
2a + b = {6i-2j+8k+i+j} = {7i - j + 8k}
|2a + b| = √(49 + 1 + 64) = √114
viktoriaserebrian:
можно пояснение к 1 заданию
Делим числитель и знаменатель на n в старшей степени, то есть на n^2. Под кубический корень попадает (n^2)^3 = n^6
При вычислении продела при n --> oo все маленькие дроби типа n/n^2, 1/n^2, 5/n - все обращаются в 0.
спасибо
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: pdp681050
Предмет: Математика,
автор: mudrec2009
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: аяжан202