Предмет: Математика,
автор: Blambum
Решите пожалуйста, задание с егэ профиль
Приложения:
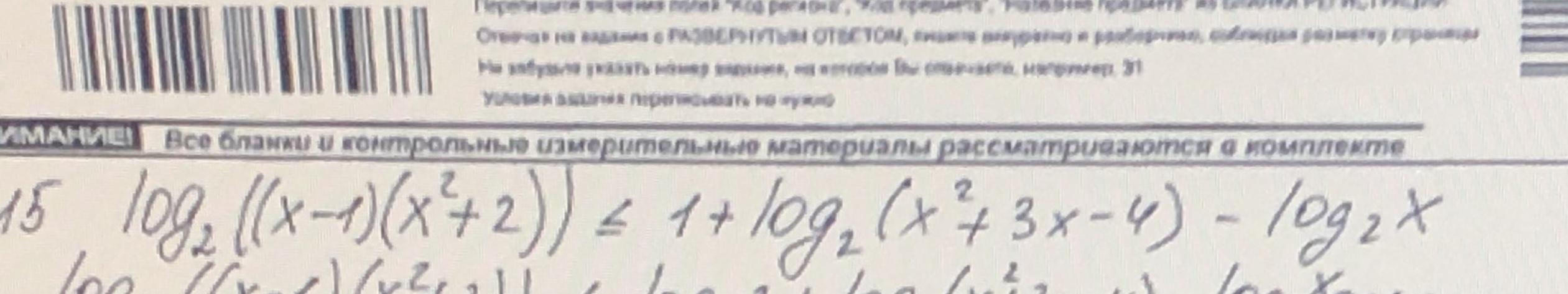
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Приложения:

oraz2002:
Если я смог вам помочь, прошу отметить ответ, как лучший !
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: rileyyyy
Предмет: Математика,
автор: sas19876068
Предмет: Русский язык,
автор: kakurakaforehead
Предмет: Математика,
автор: nikita785
Предмет: Математика,
автор: полина10001