Предмет: Алгебра,
автор: Роман1233212002
Срочно. Алгебра! С понятным решением.
Приложения:
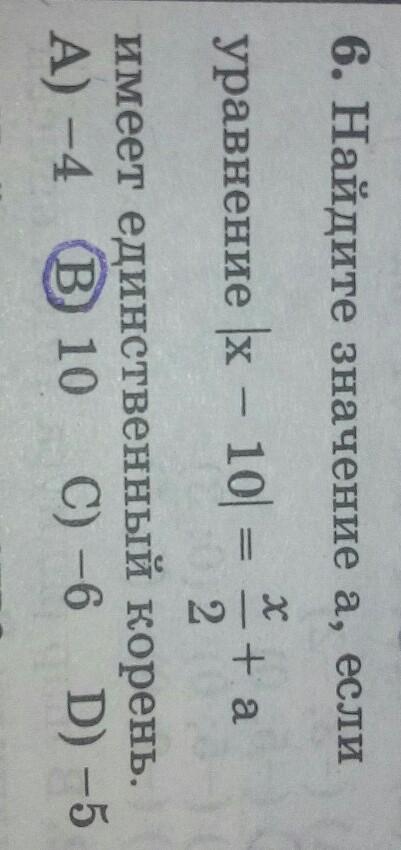
Ответы
Автор ответа:
1
Если правая часть 0.5x + a < 0 ⇒ уравнение решений не имеет.
Если 0.5x + a > 0 , то уравнение имеет два действительных корня.
Остается 0.5x + a = 0 ⇒ x = -2a.
|-2a - 10| = 0 ⇒ при a = -5 получится корень равный 10.
Роман1233212002:
хау, я то оказывается правильно решил) думал что х=-5)
Автор ответа:
1
Ответ: уравнение имеет единственный корень при a= -5 .
Объяснение:
Уравнение имеет два решения:
и
.
Если , то решение будет одно, так как равенство
возможно только в случае
.
Тогда и .
Похожие вопросы
Предмет: История,
автор: den4ik2277
Предмет: История,
автор: nastya6372600
Предмет: Математика,
автор: kamilashagirova2010
Предмет: Математика,
автор: Voeditel