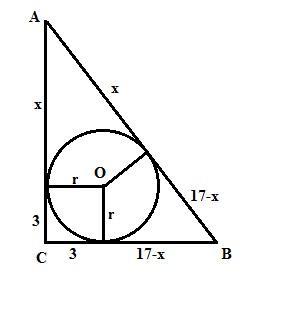
около круга с радиусом 3 описан прямоугольный треугольник, гипотенуза которого равна 17. Найдите площадь этого треугольника
Ответы
Ответ:
60
Объяснение:
2 умножим на r и с переведем в ту сторону у нас получится:
2r+c=a+b
если возвести обе стороны в квадрат тогда получится
4*r^2 + 2*2r*c+c^2=a^2+2*a*b+b^2
сокращаем и ставим значения r и c в свои места
4*9+2*2*3*17=2*a*b
2*a*b=240
a*b=120
а площадь прямоугольного треугольника равна S=a*b/2
Значит S=60
Ответ:
60 ед²
Объяснение:
Пусть прямоугольный треугольник АВС. Угол С=90°. Точка касания делит гипотенузу на отрезки: х и 17-х. Отрезки катетов от вершин А и В до точек касания равны х и 17-х, как касательные, проведенные из одной точки. Отрезки катетов от вершины С до точек касания равны радиусу вписанной окружности, то есть равны 3. Тогда катеты равны х+3 и 17-х+3 = 20-х. По Пифагору:
(х+3)² + (20-х)² = 17² => x² - 17х +60 =0. =>
х1=5, х2 =12. => катеты равны 8 и 15 ед. в обоих случаях.
Sabc = (1/2)*8*12 = 60 ед².