Предмет: Алгебра,
автор: secondmanaccount
Помогите решить уравнение
Приложения:
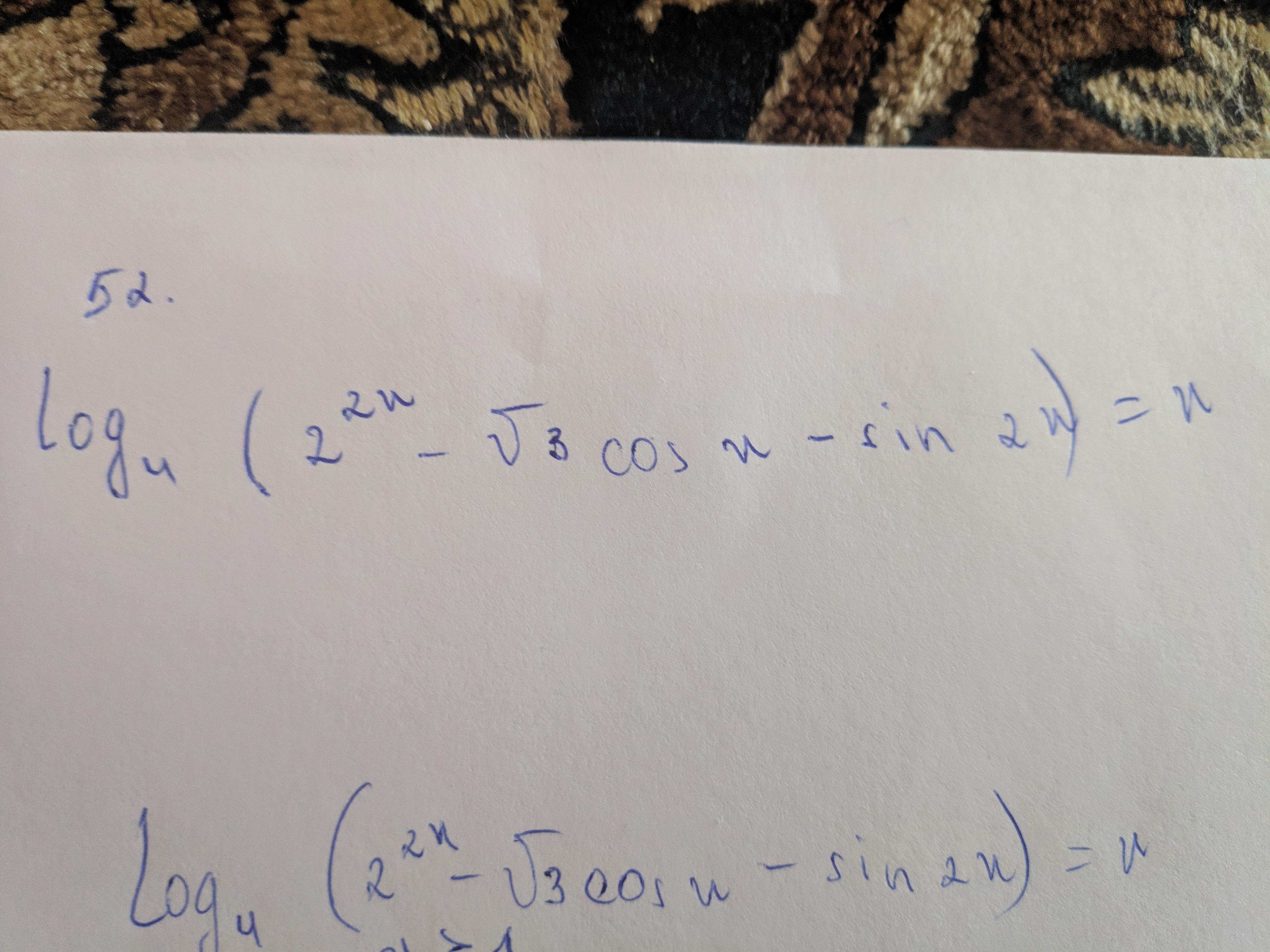
Ответы
Автор ответа:
0
Удачи и успехов)!
Похожие вопросы
Предмет: Химия,
автор: rysevaroslav76
Предмет: Биология,
автор: denismixno14
Предмет: Физика,
автор: ANYAm4788
Предмет: Математика,
автор: Jessschung
Предмет: История,
автор: Аноним