Предмет: Алгебра,
автор: onexochu
Срочно помощь нужна
Приложения:
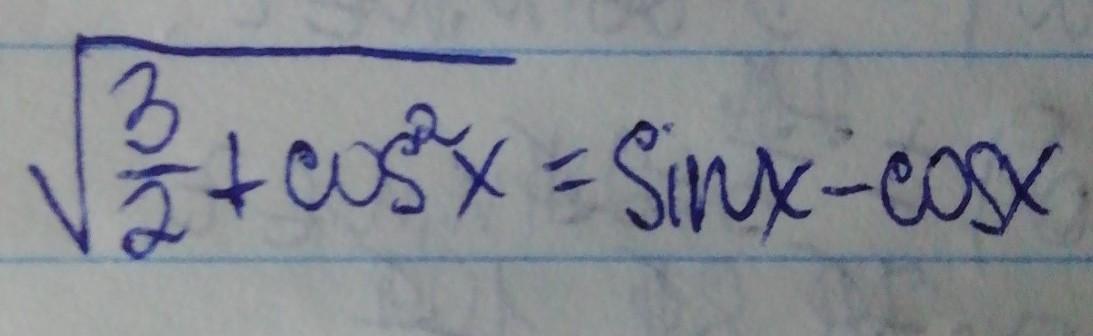
Ответы
Автор ответа:
1
Наложим ограничения на переменную х.
Из первого неравенства видно, что правая часть должна быть больше или равна корню из 3/2.
Теперь методом интервалов находим подходящий промежуток
Теперь проверим на ОДЗ и получим окончательный ответ
SergFlint:
Теперь проверим на ОДЗ и получим окончательный ответ.
ОДЗ xϵR, и нмчего проверять не надо, а в целом всё верно.
Похожие вопросы
Предмет: Алгебра,
автор: 22022006juragmailcom
Предмет: Математика,
автор: dariamyronova
Предмет: Русский язык,
автор: liyaraimmulova
Предмет: Литература,
автор: ladyaridan
Предмет: География,
автор: aminkuznetcov