Question

Срочно!!
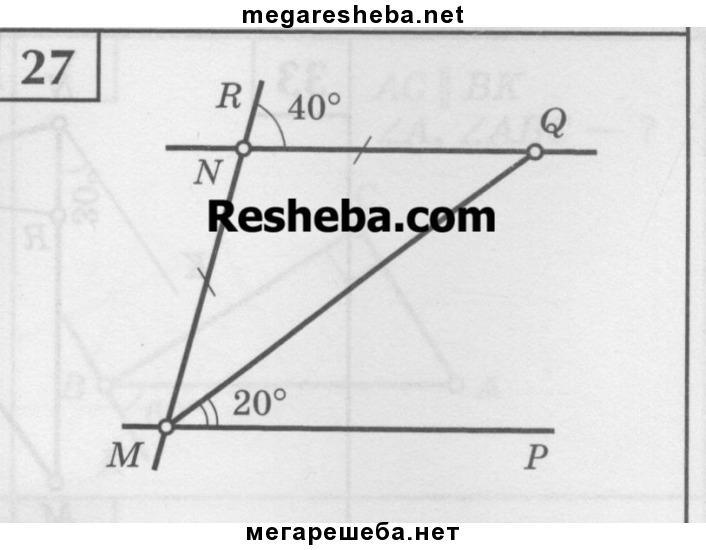
Надо доказать, что прямые NQ и MP параллельны!

Answer 1

Ответ:

1)р-м ΔMNQ

MN = NQ → ΔMNQ - равнобедренный → ∠NMQ = ∠NQM

∠RNQ = 40° → ∠NMQ+∠NQM = 40°

∠NMQ = ∠NQM = 20°

2)∠NMP = ∠NMQ+∠QMP = 20°+20° = 40°

3)∠RNQ = ∠NMP = 40°

∠RNQ и ∠NMP - соответственные при секущей RM → NQ║MP.

Answer 2

Доказательство:

1. ∠RNQ - внешний угол Δ QNM при вершине N, тогда по теореме он равен сумме двух равных углов при основании равнобедренного треугольника, не смежных с ним:

∠RNQ = ∠NQM + ∠NMQ = 2·∠NQM

40° = 2·∠NQM

∠NQM = 20°.

2. ∠NQM = ∠QMP = 20°, эти  углы являются внутренними накрест лежащими при прямых  NQ и MP  и секущей QM, тогда по признаку NQ ║ MP, что и требовалось доказать.