Question

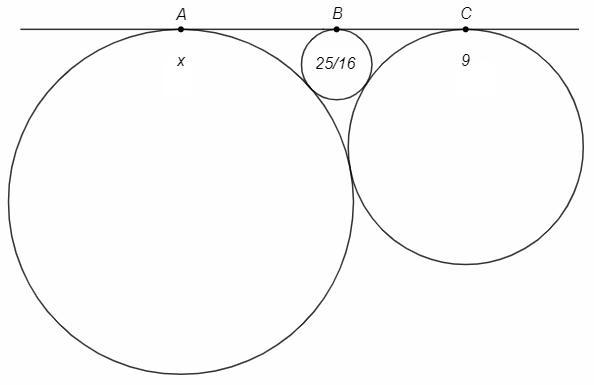
Две окружности радиусами 9см и Хсм сопрекасаются внешне. К этим окружностям проведена внешняя совместная касательная, и в созданный при этим криволинейный треугольник вписана окружность радиусом 25/16 см. Найдите радиус Х неизвестной окружности.

Answer 1

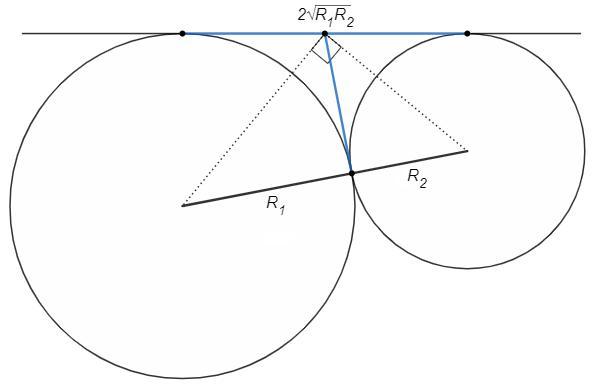
Две окружности касаются внешним образом и имеют общую внешнюю касательную. Найдем расстояние между точками касания на прямой.

Отрезки касательных из одной точки равны (синие отрезки). Центры окружностей лежат на биссектрисах углов, образованных касательными. Угол между биссектрисами смежных углов - прямой. Точка касания окружностей лежит на линии центров. Радиусы, проведенные в точку касания, перпендикулярны касательной. Таким образом синий отрезок является высотой из прямого угла и равен среднему пропорциональному проекций катетов, √(R1*R2).

Расстояние между точками касания на прямой равно 2√(R1*R2).

В задаче три пары аналогичных окружностей.

AB+BC=AC => 2√(x*25/16) +2√(9*25/16) =2√(9x) <=> 7√x =15 <=> x=225/49