Предмет: Математика,
автор: hxhdhdhd41ujdhdu685
помогите решить задачу
Приложения:
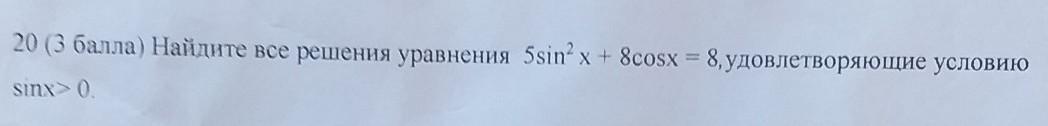
Ответы
Автор ответа:
0
Ответ:
x=arccos(3/5)+2pi*k, k∈Z.
Пошаговое объяснение:
Решим первое уравнение:
1) Заменим синус на косинус, используя тригонометрическое тождество:
5(1-cos^2(x))+8cosx=8
5-5cos^2(x)+8cosx=8
5cos^2(x)-8cosx+3=0 - квадратное уравнение относительно cosx
cosx=1 или cosx=3/5
Если cosx=1, то sinx=0 - система решений не имеет.
Если cosx=3/5 (I и IV четверти), то x=+-arccos(3/5)+2pi*k, k∈Z, но sinx>0, поэтому рассматривается только I четверть, т.е. x=arccos(3/5)+2pi*k, k∈Z.
Похожие вопросы
Предмет: Биология,
автор: semenov022009
Предмет: Литература,
автор: razboynik570
Предмет: Литература,
автор: arinaabdhub
Предмет: Литература,
автор: majorrr777
Предмет: Математика,
автор: voronovanastya2004