Предмет: Геометрия,
автор: Dankamn16
Даны вершины треугольника А(3, –5), В(–3, 3), С(–1, –2). Определить длину его биссектрисы, проведенной из вершины А.
Ответы
Автор ответа:
0
Найдем AB:
Аналогично AC=5, BC=
Найдем биссектрису:
Ответ:
Автор ответа:
2
Решение задания приложено
Приложения:

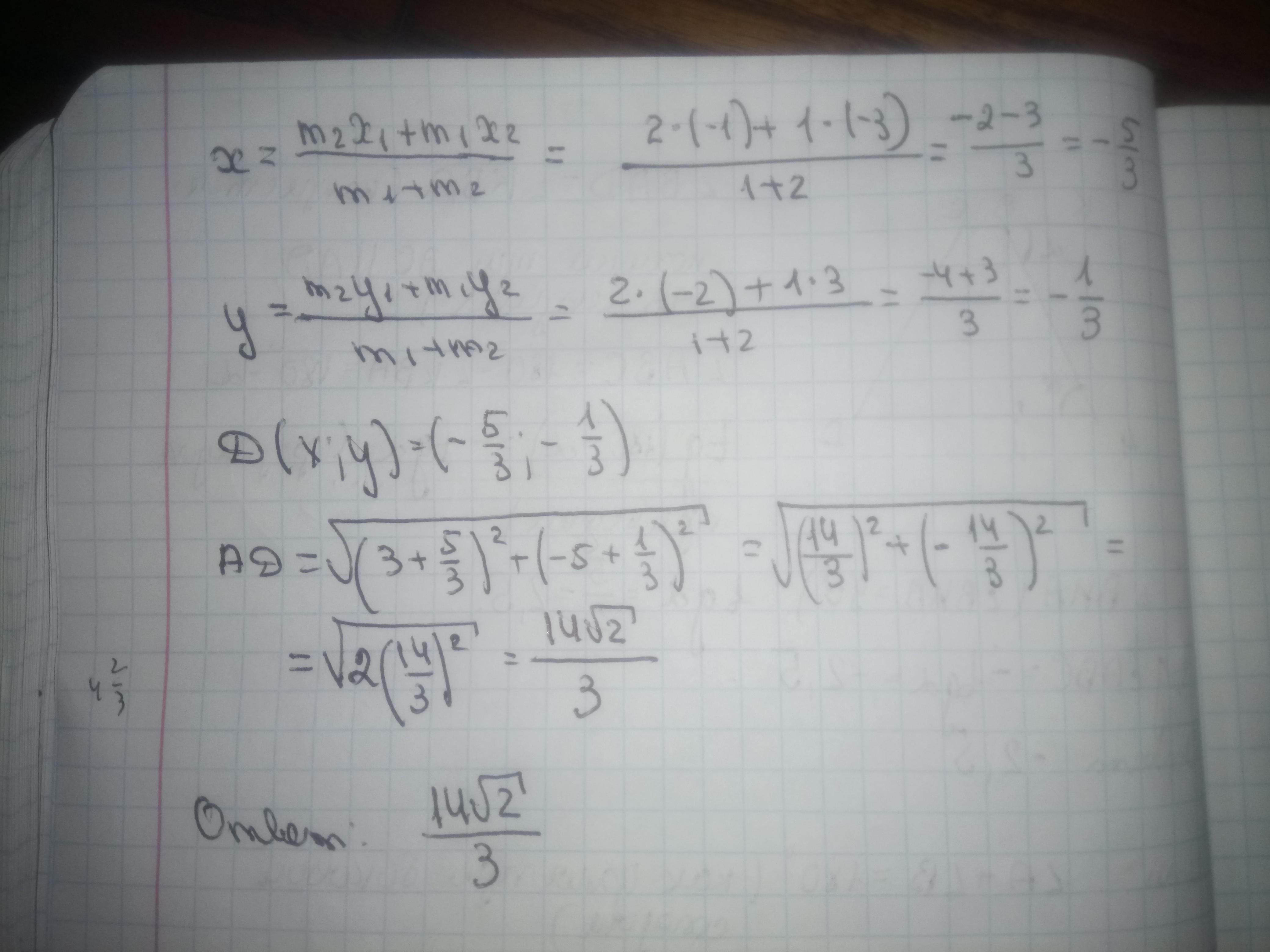
Спасибо огроменное!!
Похожие вопросы
Предмет: Обществознание,
автор: reyyywei19
Предмет: Другие предметы,
автор: innamartynova87
Предмет: Математика,
автор: vladtamkaev
Предмет: Математика,
автор: katipasla
Предмет: Математика,
автор: vovamoiseenko
Но в рамке не открывается почему-то((