Предмет: Математика,
автор: B3ndeR
Вычислить приближенно с помощью дифференциала (1,98/2,02)^1/5
Ответы
Автор ответа:
0
Ответ:
Ответ внизу на фото
Пошаговое объяснение:
Приложения:
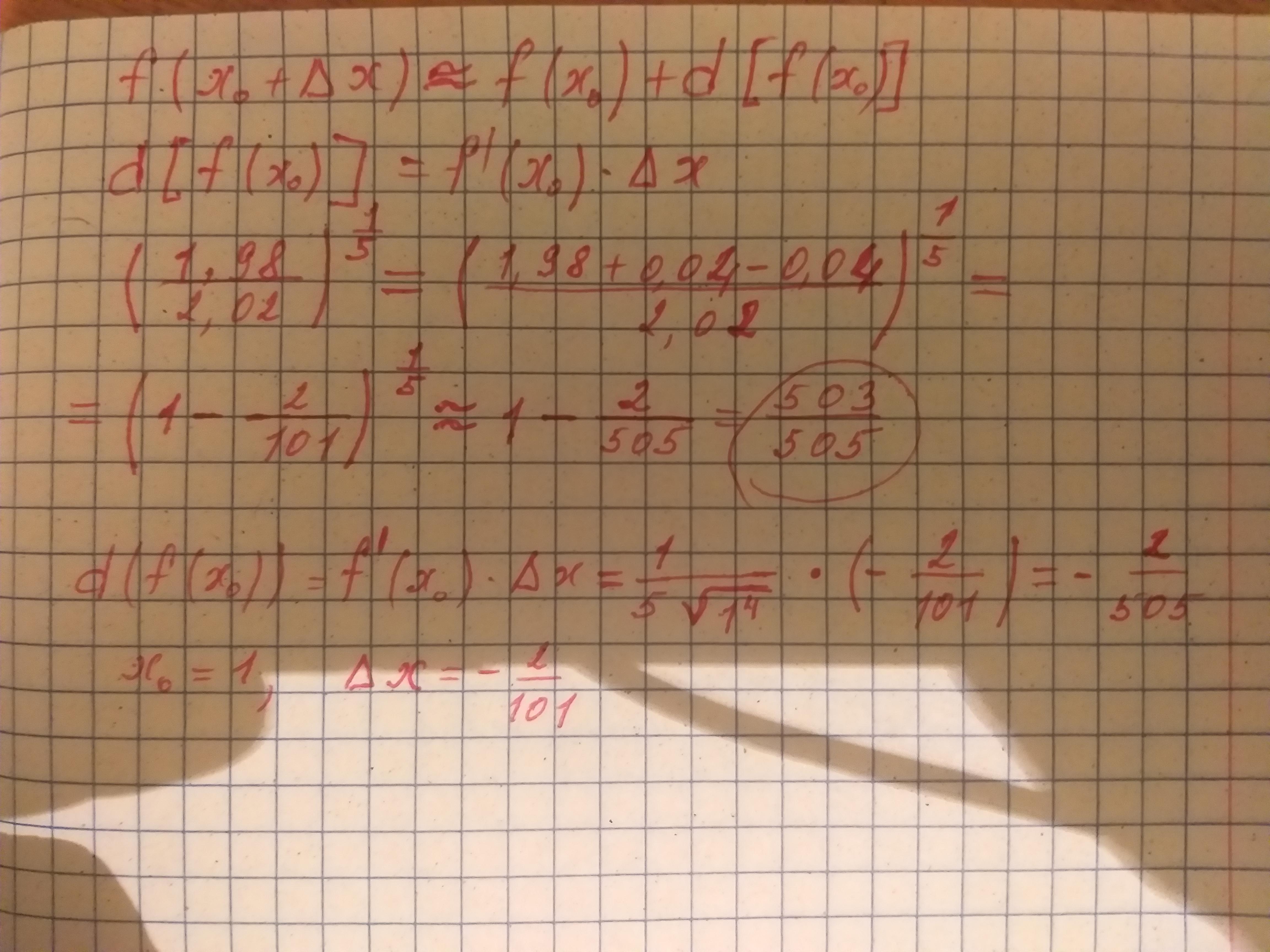
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: История,
автор: VMariha
Предмет: Русский язык,
автор: kurahh
Предмет: Математика,
автор: ochkobarana335
Предмет: Обществознание,
автор: sergeenkoandre
Предмет: Математика,
автор: 0slastena0