Предмет: Математика,
автор: boyarkinnikita
Нужно срочно решить задачу Коши.
Приложения:

Ответы
Автор ответа:
1
Решение второго задания на листке ===>>
Приложения:
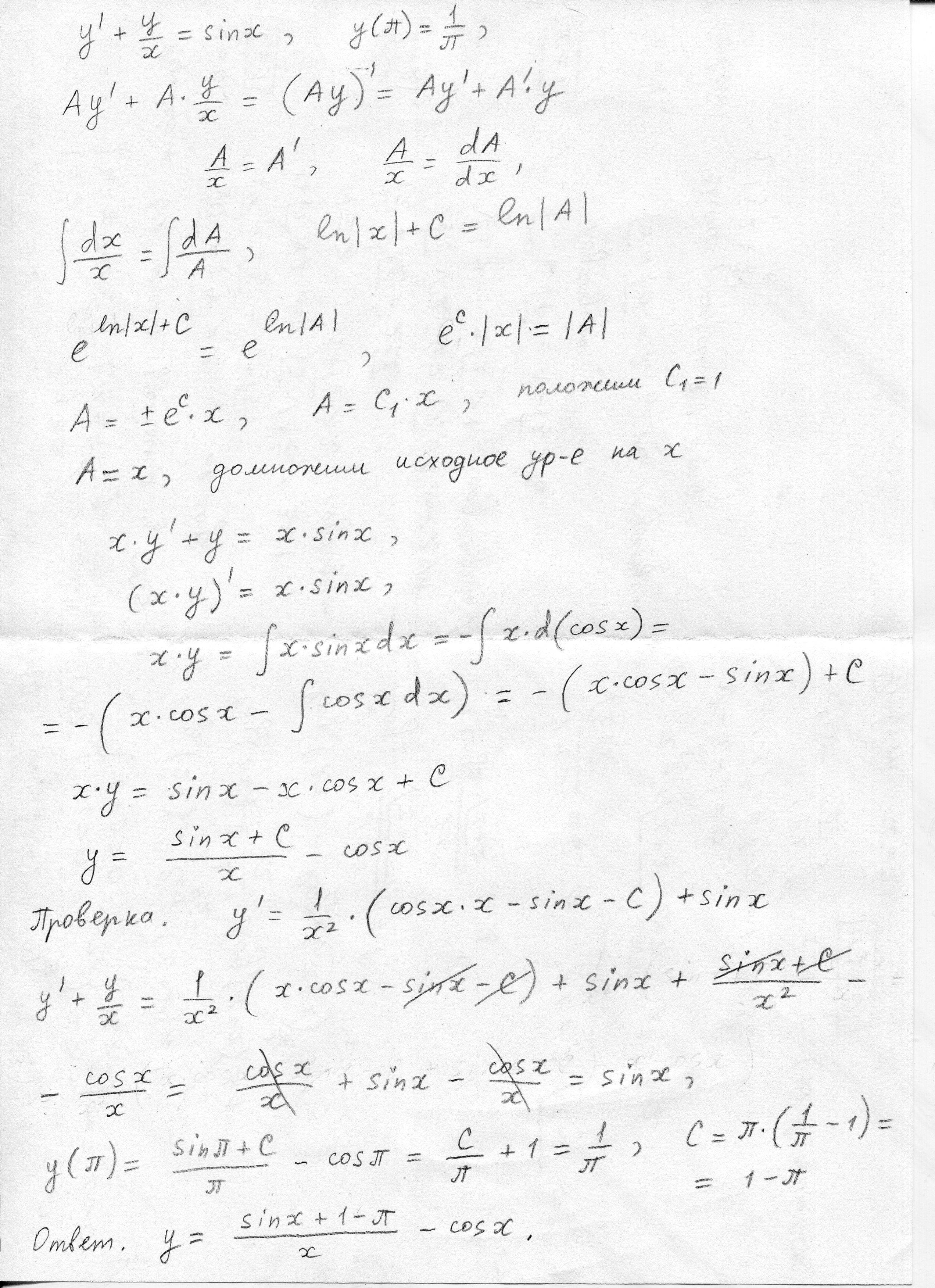
Автор ответа:
1
Похожие вопросы
Предмет: Другие предметы,
автор: Morgan2282222
Предмет: Геометрия,
автор: ksusaarovaa5
Предмет: Алгебра,
автор: hhhhhhshssffa
Предмет: Обществознание,
автор: Milena19802004
Предмет: Биология,
автор: alexeis4292