Question

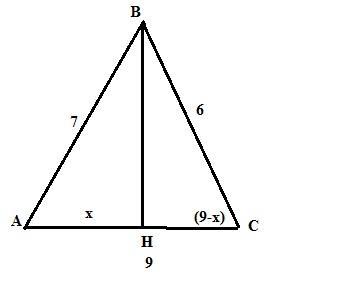
дан треугольник ABC. AB=7, BC=6, AC=9. BH - высота. Найти BH, AH, HC

Answer 1

Ответ:

Пошаговое объяснение:

1) Найдём площадь треугольника АВС по формуле Герона:

S = $\sqrt{p(p-a)(p-b)(p-c)}$ , где p - полупериметр ($\frac{1}{2} (a+b+c)$)

S = $\sqrt{11*4*5*2}$ =2√110

2) Воспользуемся формулой площади через высоту:

S = $\frac{1}{2} ah$, где a = AC, h = BH

2√110 = $\frac{1}{2}$·9 · BH

BH = $\frac{4\sqrt{110} }{9}$

3) Работаем в треугольнике ABH:

по теореме пифагора $AB^{2}$ = $AH^{2}$ + $BH^{2}$

49 = $AH^{2}$ + $\frac{16*110}{81}$

AH = $\sqrt{49-\frac{1760}{81} }$

4) HC = AC - AH

HC = 9 - $\sqrt{49 - \frac{1760}{81} }$

Answer 2

Ответ:

АН = 5и2/9 ед. НС = 3и7/9 ед.  ВН = (4√110)/9 ед.

Пошаговое объяснение:

В прямоугольных треугольниках АВН и СВН катет ВН (высота данного нам треугольника) - общий. Примем АН=х, тогда НС=9-х.

Выразим ВН из двух прямоугольников по Пифагору и приравняем эти выражения:

7² - х² = 36 - (9-х)²  =>  49 - х² = 36 - 81 + 18х - х²  =>

9х = 47.  =>  х = АН = 5и2/9 ед. Тогда НС = 9 - 5и2/9 = 3и7/9 ед.

Найдем ВН:

ВН² = 49 - (5и2/9)² = 49 - 2209/81 = 1760/81.

ВН = 4√110/9 ед.