Question

Найти биссектрису прямого угла треугольника, если гипотенуза его равна с, а острый угол а. Пожалуйста!

Answer 1

Ответ:

решение представлено на фото

Answer 2

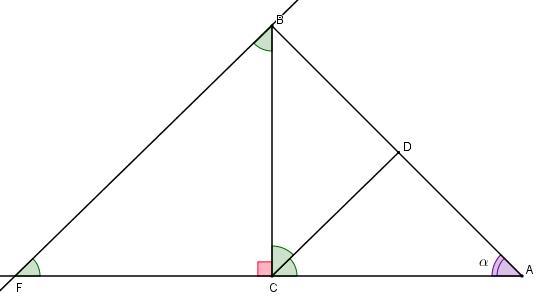
Пусть дан ABC - прямоугольный треугольник; AB = c; ∠A = α. Поскольку CD — биссектриса прямого угла C, то ∠BCD = ∠DCA = 45°. Из треугольника ABC: AC = c · cosα и BC = c · sinα.

Из точки В проведём прямую, параллельную CD, и продолжим, AC до пересечения с этой прямой в точке F.

∠FBC = ∠BCD как накрест лежащие при FB || CD и секущей BC.

Тогда ∠BFC = ∠FBC = 45°  ⇒  ΔBFC — равнобедренный прямоугольный треугольник ⇒ BC = FC = c · sinα;

FB = BC√2 = c · √2 · sinα

Из подобия треугольников FBA и CDA:

  $\dfrac{FB}{CD}=\dfrac{AF}{AC}~~~\Rightarrow~~~\dfrac{FB}{CD}=\dfrac{FC+AC}{AC}~~~\Rightarrow~~~\dfrac{c\sqrt{2}\sin\alpha}{CD}=\dfrac{c(\sin\alpha+\cos\alpha)}{c\cos \alpha}\\ \\ \\ CD=\dfrac{c\sqrt{2}\sin\alpha\cos\alpha}{\sin\alpha+\cos\alpha}~~~\Rightarrow~~~ \boxed{CD=\dfrac{c\sin2\alpha}{\sqrt{2}(\sin\alpha+\cos\alpha)}}$