Предмет: Алгебра,
автор: yabuzulu22
Помогите решить уравнение!!!
Даю 50 баллов
Где N=17
Приложения:
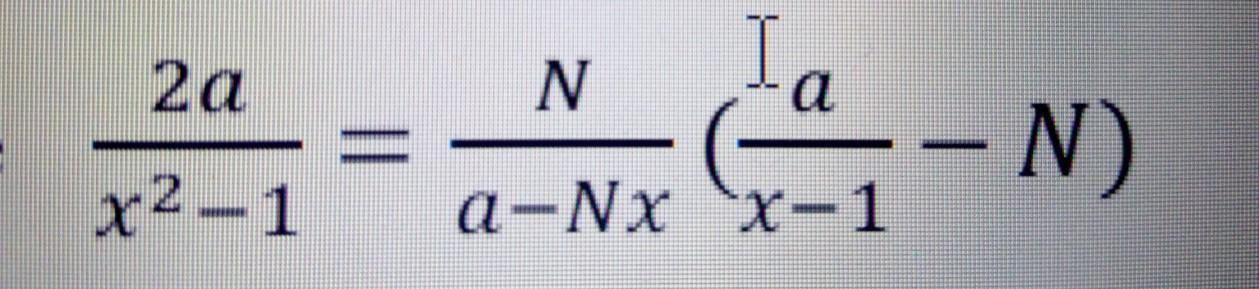
Simba2017:
так там еще а...
с параметром
Ответы
Автор ответа:
2
Ответ:
Объяснение:
2a/(x^2 - 1) = 17/(a - 17x)*(a - 17x + 17)/(x - 1)
ОДЗ x ≠ 1; x ≠ - 1; x ≠ a/17
Умножаем все на общий знаменатель (a-17x)(x-1)(x+1)
2a(a - 17x) = 17(x+1)(a+17-17x)
2a^2 - 34ax = 17(ax+a+17x+17-17x^2-17x)
2a^2 - 34ax = - 289x^2 + 17ax + 17a + 289
289x^2 - 51ax + (2a^2 - 17a - 289) = 0
Обычное квадратное уравнение с параметром.
D = 51^2*a^2 - 4*289(2a^2 - 17a - 289) = 289*(9a^2 - 8a^2 + 68a + 1156) =
= 289*(a^2 + 68a + 1156) = [17*(a+34)]^2
Так как D есть точный квадрат, то он неотрицателен при любом а.
При а = - 34 будет D = 0 и
x = 51a/(2*289) = - 3*17*2*17/(2*17^2) = - 3
При всех других а, с учетом ОДЗ, будет
x1 = [51a - 17(a+34)]/(2*289) = [3a - (a+34)] /34 = (2a-34)/34 = a/17 - 1
x2 = [3a + (a+34)]/34 = (4a+34)/34 = 2a/17 + 1
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Литература,
автор: sashundezlol
Предмет: Алгебра,
автор: NoobLatunch2008
Предмет: Математика,
автор: Аноним
Предмет: Химия,
автор: arnass02