Question

Помогите решить:

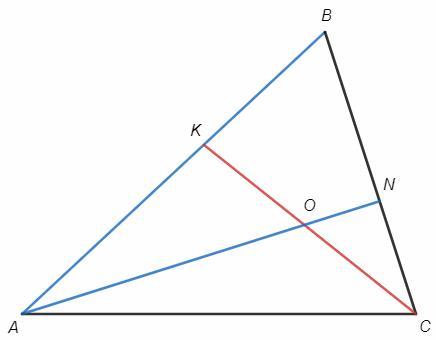
1) В треугольнике АВС точка К лежит на АВ, а точка N – на ВС, причем АК:КВ = 3:2, а BN:NC = 3:2. Отрезки CK и AN пересекаются в точке О. Найти АО:ОN.

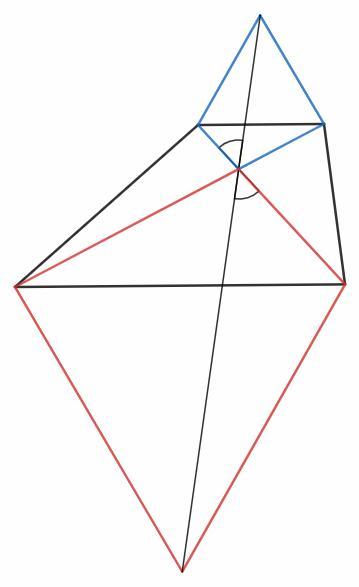
2) На каждом из оснований трапеции ABCD построены вне трапеции равносторонние треугольники. Докажите, что прямая, соединяющая вершины треугольников, не лежащие на основаниях трапеции, проходит через точку пересечения диагоналей трапеции.

Answer 1

1) По теореме Менелая

BK/KA *AO/ON *NC/CB =1

2/3 *AO/ON *2/5 =1

AO/ON =15/4

2) Треугольники, образованные диагоналями на основаниях трапеции, подобны (по накрест лежащим углам при параллельных). Правильные треугольники очевидно подобны. Таким образом синий и красный четырехугольники подобны. Отрезки от вершин до точки пересечения диагоналей являются соответствующими в подобных фигурах и составляют равные углы с соответствующими сторонами. Отрезки отложены от диагонали на равные углы и составляют развернутый угол, то есть прямую.