Предмет: Геометрия, автор: mrfirefox132

Дан выпуклый четырехугольник ABCD. E середина BC. F середина AD. BD пересекает EF в точке H. AC пересекает EF в точке G. Доказать что EF делит AC и BD в одинаковом отношении. ( Я дошёл до того что площадь BGH/GHD = площадь CGH/AGH)

mrfirefox132: Почему там одна высота я вот этого не понимаю

Simba2017: ладно , жди жертеж

mrfirefox132: Спасибо)

Simba2017: промахнулась я немного, придется выводить...

Simba2017: твои сомнения и мне передались, но все по-моему верно

antonovm: еще одно решение ( без площадей )

siestarjoki: Очевидно по теореме Менелая.

siestarjoki: i.imgur.com/eqGopzb.png

siestarjoki: BE/EC *CG/GA *AX/XB =1
BH/HD *DF/FA *AX/XB =1

siestarjoki: Если EF параллельна AB, то является средней линией в BCA и BDA.

Ответы

Автор ответа: Simba2017

..................................................................

Приложения:

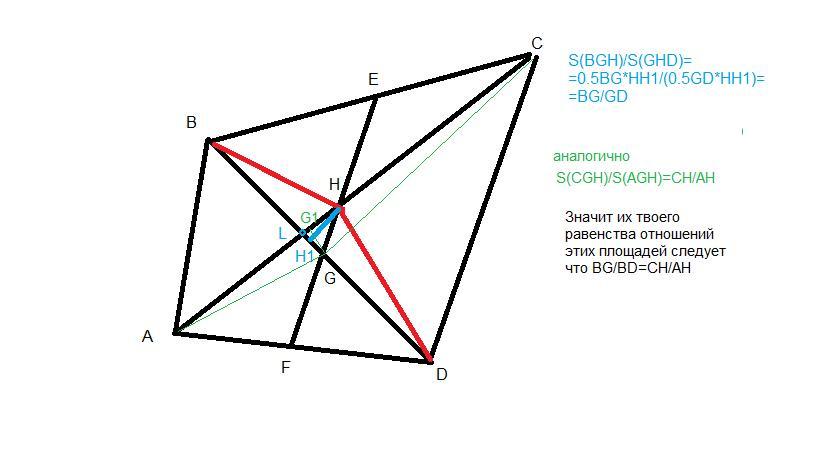
mrfirefox132: то есть в agh и ghc одна высота?

Simba2017: GG1-высота в треугольниках AGH и CGH

mrfirefox132: ну то есть в cgh высота за треугольником

Simba2017: поэтому отношение их площадей будет равно отношению их оснований AH и HC

mrfirefox132: она не в самом треугольнике

Simba2017: да, он же тупоугольный

mrfirefox132: а ну все тогда понятно

Simba2017: поэтому высота к основанию, лежащему против тупого угла лежит вне треугольника

mrfirefox132: да все понял спасибо

Simba2017: удачи)

Автор ответа: antonovm

Ответ:

Объяснение: Решение : ////////////////////////

Приложения:

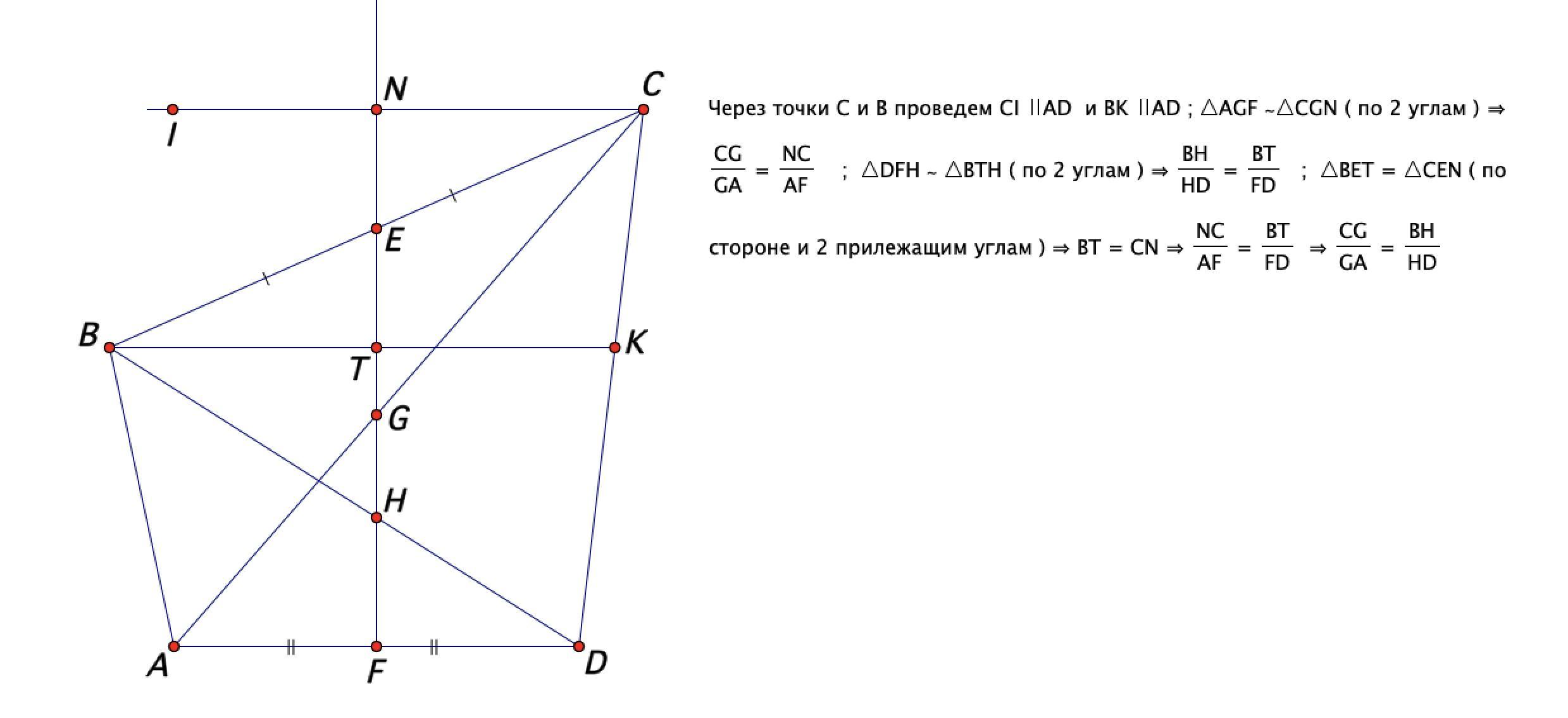
Simba2017: лаконично )

mrfirefox132: мда классное решение учитывая что я писал про то что нашел отношение площадей)

mrfirefox132: но впринципе тоже понятно

Simba2017: лучшее у модератора

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: История, автор: varazaricanska

СРОЧНО!
Розставте у хронологічній послідовності події: а) відкриття в Одесі Новоросійського університету, б) створения першої західноукраїнської опери «Купало»; в) відкриття у Кисві Південно-Західного відділу Російсыкого географічного товариства; г) створення першої української опери- «Запорожець за Дунаєм».

6 лет назад

Предмет: Українська література, автор: sorokad341

гітчі маніто закликав

6 лет назад

Предмет: Алгебра, автор: mountainpeak228

Помогите пж СРОЧНО!
7x+4y=9 та 2x+5y=-9

6 лет назад

Предмет: Алгебра, автор: ТаняПтица

УМОЛЯЮ ВАС, ПОМОГИТЕ РЕШИТЬ! НЕ ИГНОРИРУЙТЕ!!!
Известно, что. $5x^{2}y^{3} = -7$ Найдите значение выражения: $2)5x^{4}y^{6}$ $1) -10x^{2}y^{3}$

9 лет назад

Предмет: Математика, автор: aslana05

УМОЛЯЮ.. У МЕНЯ УЖЕ 2 ЧАСА НОЧИ
Температура была утром и тд
ном 535

9 лет назад