Question

В каком отношении делит площадь треугольника прямая, проходящая через центр тяжести параллельно одной из его сторон

Answer 1

Ответ:

Объяснение:

В каком отношении делит площадь треугольника прямая,

Answer 2

Объяснение:

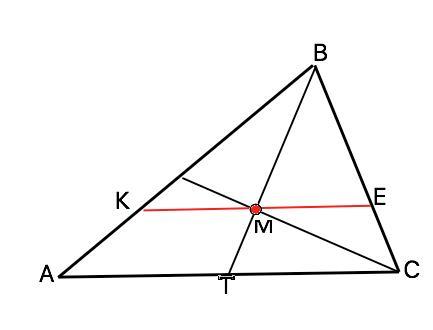
   Центром тяжести треугольника является точка пересечения его медиан. Пусть в треугольнике АВС  медиана ВТ, точка М- центр тяжести,, КЕ проходит через М и параллельна АС.  

 В треугольниках АВС и КВЕ угол при вершине В общий,  соответственные углы при пересечении АС и КЕ боковыми сторонами равны  ( КЕ||АС, АВ и СВ - секущие). Следовательно, ∆ КВЕ подобен ∆АВС.  По свойству медиан ВМ:МТ=2:1, ⇒ ВЕ:ЕС=2:1, а k=ВЕ:ВС=2/3      Отношение площадей подобных фигур равно квадрату коэффициента подобия.  

Ѕ(КВЕ):Ѕ(АВС)=k²=4/9.

Примем коэффициент отношения площадей равным а. Тогда Ѕ(АКЕС)=Ѕ(АВС)-Ѕ(КВЕ)=9а-4а=5а  ⇒  Ѕ(КВЕ):Ѕ(АКЕС)=4а:5а=4/5