Предмет: Математика,
автор: Аноним
70 Б. Здравствуйте. Ищу помощи с решением уравнения! Найти общий интеграл однородного дифференциального уравнения первого
порядка
Приложения:
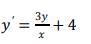
Ответы
Автор ответа:
1
Первый способ.
Так как диф. уравнение однородное, то для него осуществляется замена y = ux, тогда y' = u'x + u, имеем:
Выполнив обратную замену u = y/x, имеем:
Получили общий интеграл.
Второй способ.
Умножим левую и правую части уравнения на , которое определяется соотношением:
Проинтегрируем обе части уравнения
Получили общее решение.
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Українська мова,
автор: gguogamggdf
Предмет: Химия,
автор: savchsash
Предмет: Алгебра,
автор: akiraNight
Предмет: Физика,
автор: BlackPrince1