Предмет: Математика,
автор: materialsofmylife
Решите пожалуйста , высшая математика кажется, в интернете смотрю похожие но все равно ответ не получается :(
Приложения:
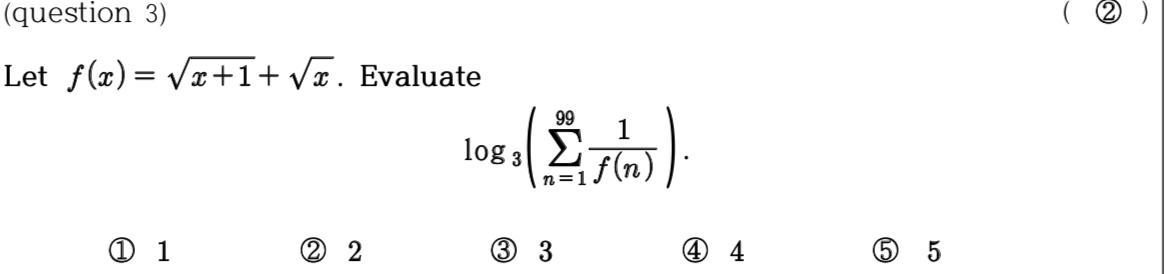
Ответы
Автор ответа:
1
Окончательно имеем
Похожие вопросы
Предмет: Математика,
автор: Gnomik2548
Предмет: Русский язык,
автор: torontororo97
Предмет: География,
автор: alinaprokopchuk2010
Предмет: Математика,
автор: karshackov2016