Question

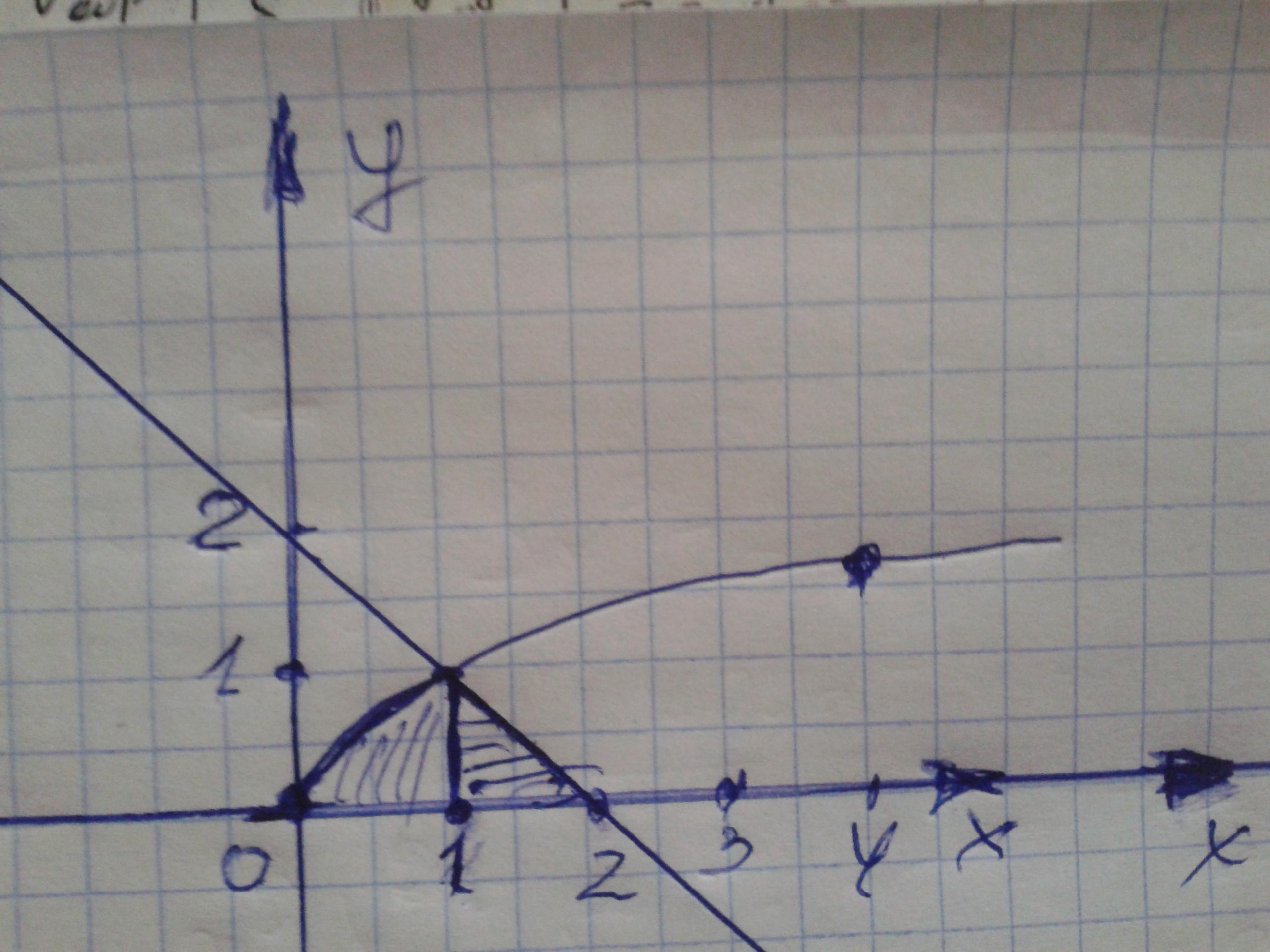
Вычислить площадь фигуры, ограниченной линиями:
y = Vx, y = 2 - х. ось ох

Answer 1

Ответ: S≈1,167 кв. ед.

Объяснение:

y=√x     y=2-x     y=0     S=?

√x=0      x₁=0

2-x=0      x₂=2

√x=2-x      

x+√x-2=0

Пусть √x=t>0   ⇒

t²+t-2=0       D=9          √D=3

t₁=√x=1       (√x)²=1²        x₃=1

t₂=√x=-2 ∉    ⇒

S₁=₀∫¹(√x)dx=((2/3)*x³/²) ₀|¹=(2/3)*1³/²-0=2/3.

S₂=₁∫²(2-x)dx=(2x-(x²/2))  ₁|²=(2*2-(2²/2)-(2*1-(1²/2))=4-2-(2-(1/2)=2-1,5=0,5.

S=S₁+S₂=(2/3)+0,5≈0,667+0,5≈1,167.