Найти наибольшее значение биссектрисы CL остроугольного треугольника ABC, если известно что AB=c, а радиус описанной около треугольника окружности равен R.
Ответы
Рассмотрим ΔАВС и ΔАВС1. Продолжим биссектрисы CL и С₁L₁ до пересечения с описанной окружностью в точке Р. ∠АСP = ∠ВСР ⇒ ∪АР = ∪ВР . Хорды, стягивающие равные дуги, равны ⇒ АР = ВР
Пусть СР будет больше С₁Р, тогда проекция отрезка РL на прямую АВ меньше проекции отрезка РL₁
С₁L₁ = C₁P - PL₁ < C₁P - PL < CP - PL = CL
Конечно, можно сравнивать и 3, и 4 таких отрезков, но не будем терять время. Поэтому, чем ближе искомая биссектриса к диаметру , тем она длиннее. Таким образом, наибольшее значение биссектрисы будет у равнобедренного треугольника ABC₂ , С₂L₂ - искомая
Перпендикуляр, опущенный на АВ, проходит через его середину и центр описанной окружности.
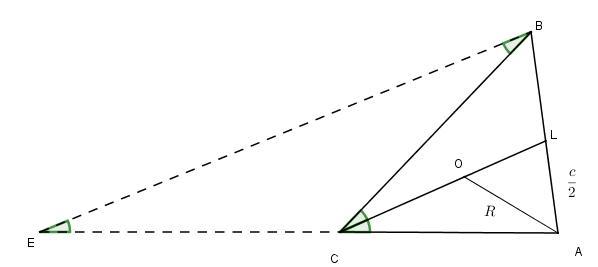
В ΔАОL₂: OL₂= √(AO² - AL₂²) = √(R² - (c/2)²) = 0,5•√(4R² - c²)
C₂L₂ = C₂O + OL₂ = R + 0,5•√(4R² - c²)
ОТВЕТ: R + 0,5•√(4R² - c²)

Из вершины В продлим сторону параллельную CL до пересечения продления стороны АС так что EC = BC; ∠ EBD = ∠BCL = α как накрест лежащие при EB || CL и секущей BC.
∠BEC = ∠EBC ⇒ ΔEBC — равнобедренный. Из этого треугольника
EB = 2BC * cosα (высота, проведенная к ЕВ, делит на два равных прямоугольных треугольника, отсюда и легко найти).
ΔCLA ~ ΔEBA следовательно из подобия
BC = CE, тогда
Среднее гармоническое двух чисел a;b : , а среднее геометрическое -
.
. В данном случае достигает максимума, когда выполняется равенство а=b.
Т.к. α — постоянная величина ; среднее гармоническое не превосходит среднего геометрического и достигает максимума , тогда и только тогда, когда AC=BC , а значит треугольник равнобедренный, отсюда CL - высота и медиана
По т. Пифагора из треугольника OLA:
OC = OA = R, окончательно имеем: