Question

В треугольнике ABC проведена биссектриса AL. Оказалось, что AL=AB. На отрезке AL выбрана точка K так, что BK=CL. Известно, что ∠BAC=68∘. Найдите угол ABK.

Answer 1

△BAL - равнобедренный

∠ABC=(180 -68/2)/2 =73

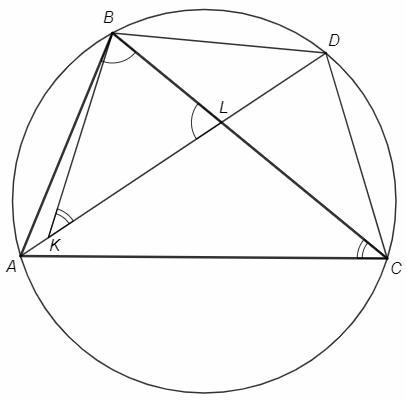
Биссектриса AL пересекает описанную окружность в точке D.

∠ADC=∠ABC, ∠BCD=∠BAD (вписанные углы, опирающиеся на одни дуги)

△BAL~△DCL (по двум углам), △DCL - равнобедренный, DC=CL

DC=BD (хорды, стягивающие равные дуги)

BK=CL=BD, △KBD - равнобедренный, ∠BKD=∠BDA=∠BCA

△LBK~△BAC (по двум углам), ∠LBK=∠BAC =68

∠ABK= ∠ABC-∠LBK =73-68 =5