Question

Вычислить площадь фигур ограниченной линиями:
y=x+2, y=x^2 - 4x+2​

Answer 1

Ответ:

Объяснение:

вот

Answer 2

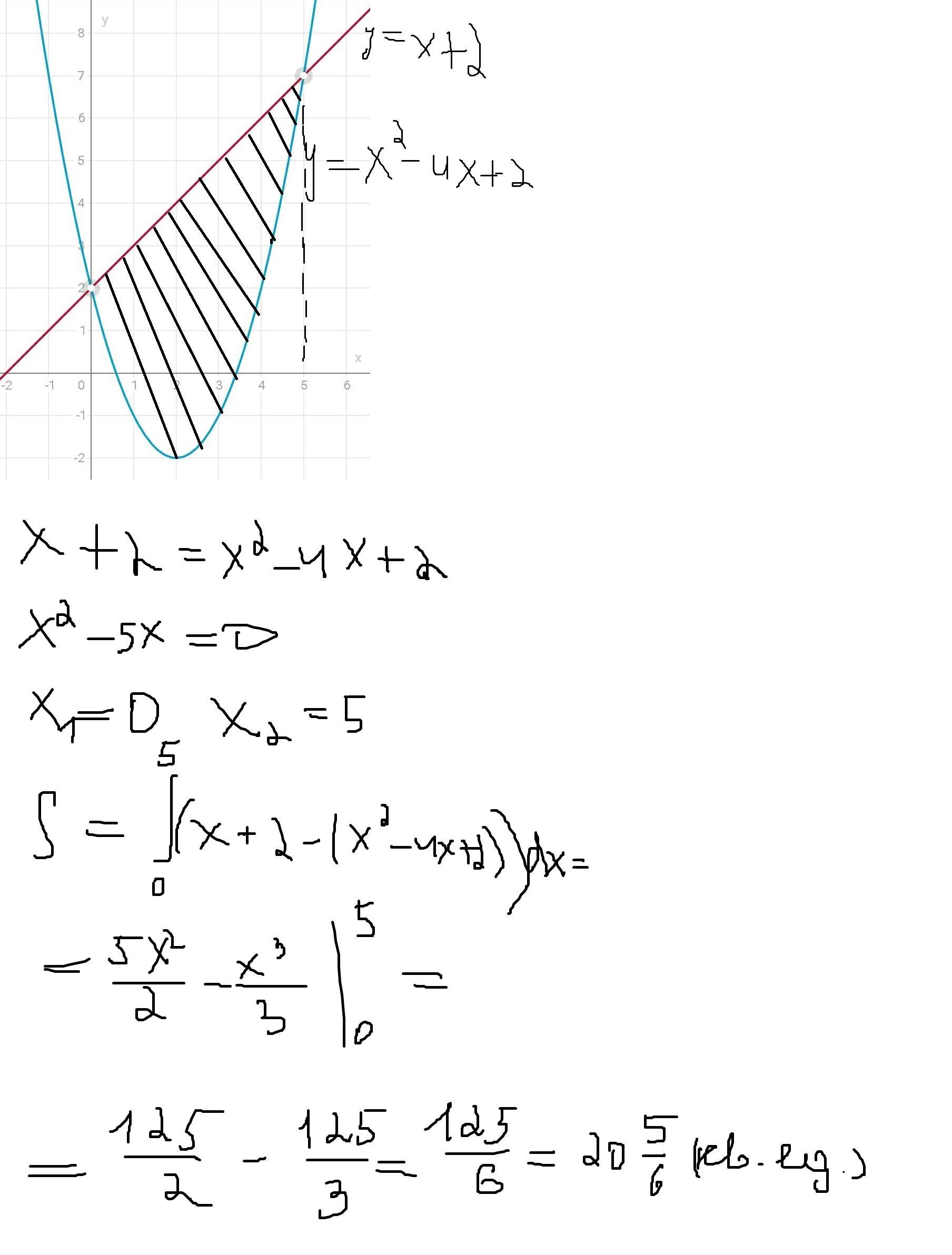
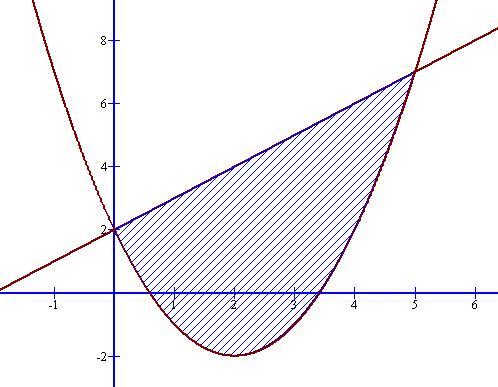
y = x +2 - прямая, проходящая через точки (0;2), (-2;0).

y = x² - 4x + 2 = (x-2)² - 2 — парабола, ветви направлены вверх. Координаты вершины параболы: (2;-2).

Найдем точки пересечения двух графиков, приравнивая их функции

x + 2 = x² - 4x + 2

x² - 5x = 0

x(x-5) = 0

x = 0

x = 5

Площадь фигуры ограниченной линиями:

$\displaystyle \sf S=\int\limits^5_0(x+2-(x^2-4x+2))dx=\int\limits^5_0(5x-x^2)dx=\\ \\ \\ =\left(\frac{5x^2}{2}-\frac{x^3}{3}\right)\bigg|^5_0=\frac{5\cdot5^2}{2}-\frac{5^3}{3}=5^3\left(\frac{1}{2}-\frac{1}{3}\right)=5^3\cdot\frac{1}{6}=\frac{125}{6}~ kB.~ed.$

Ответ: 125/6 кв. ед.