Предмет: Математика,
автор: Аноним
Прошу помочь решить уравнения! Найти частное решение дифференциального уравнения
Приложения:
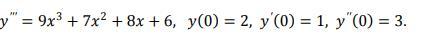
Ответы
Автор ответа:
2
Проинтегрируем почленно трижды уравнение, получим
Подставляя начальные условия, мы получим
Частное решение:
Похожие вопросы
Предмет: Английский язык,
автор: zhorzhmik
Предмет: Математика,
автор: natalya1954040960
Предмет: Українська література,
автор: doshirakdariana
Предмет: Математика,
автор: coicevalera